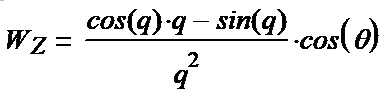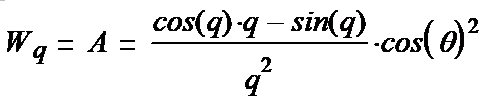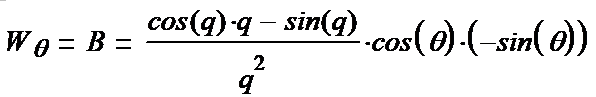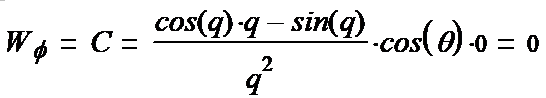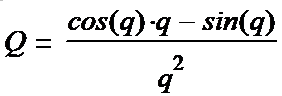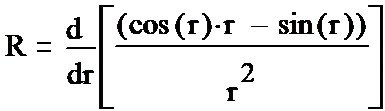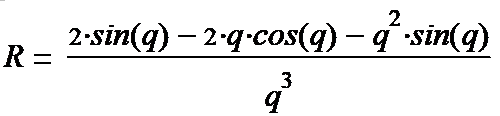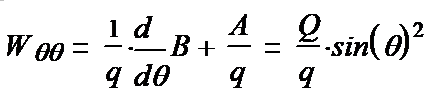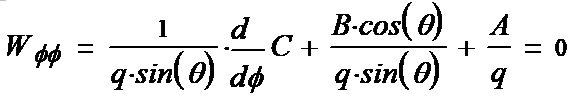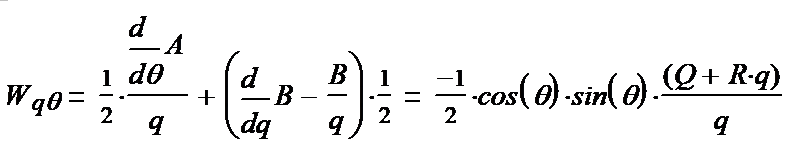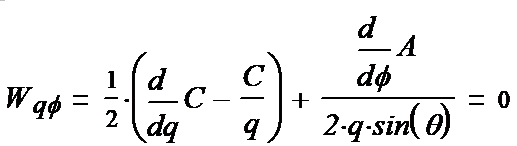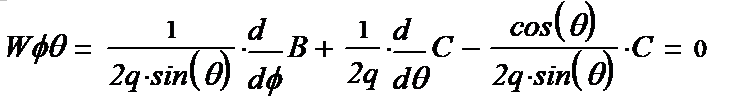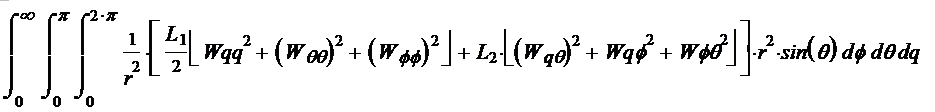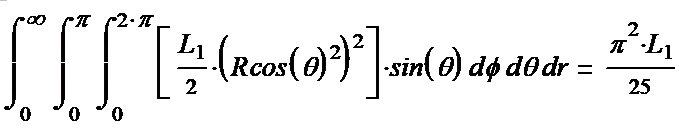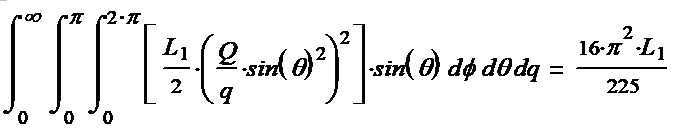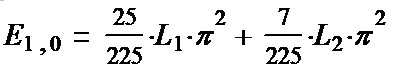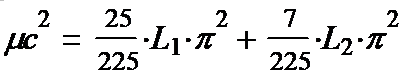Ниже эта процедура показана для простого случая  j=1  и  m=0 . Какая это частица, мы пока не знаем.
   Формула смещения в вертикально размещенном локе. Зависимость  W  от угловых координат отсутствует. Используется безразмерная радиальная координата  q=k•r. k – коэффициент, зависящий от реальной массы частицы.

(1-22*)

   Коэффициент под квадратным корнем временно опускаем. Вставим его в конце. Что такое коэффициент k. Это не более чем связующее звено между ω в колебательной части решения и радиальной координатой в функции Бесселя: ω=k*c, c-скорость света. Физика такова, что в каждой частице (в каждом решении) в силу физических причин устанавлявается своя частота бегущей по кругу волны. Физические причины определяются формой решения, и тем как происходит наматывание решения само на себя, и как вся система стабилизируется в устойчивое состояние. Также у частиц бывают возбуждённые состояния. Этот вопрос пока не исследован. Это можно только наблюдать. Таким образом все дальнейшие решения и формулы являются только иллюстрацией того состояния, в котором находятся все волновые вихри = локи = элементарные частицы.

   Имеем три компоненты смещения как в (1-13):
 

(1-23*) (1-24*) (1-25*)

   Вводим полезные обозначения:

 Выписываем компоненты тензора (1-15):

(1-26*) (1-27*)  (1-28*) (1-29*)  (1-30*) (1-31*)

   Теперь попробуем выписать формулу для энергии:

(1-32*)

Здесь: в центре, в квадратной скобке собственно выражение для плотности энергии. Справа после скобки выражение для элемента объёма. Слева перед скобкой выражение (1/r²) для закона наматывания.

   Подсчитываем эти интегралы. Вычисляем каждый по отдельности.

 

   Итак, получается шесть тройных интегралов. Слава компьютерным программам, открывающим нам доступ к познанию элементарных частиц!  Это новые горизонты науки. Получаем решение (1-33*):

 

(1-34*)

   Эта формула - нечто, связывающее упругие свойства Гукуума  (L₁,L₂)  с массой (предполагаемых!) элементарных частиц и угловой скоростью их вращения. Применяя формулу лорда Кельвина, получаем:

 

(1-35*)

Пока мы не знаем, какая это частица. Два таких уравнения для двух разных локов позволят определить L₁ и L₂ космического Гукуума.

--- ---