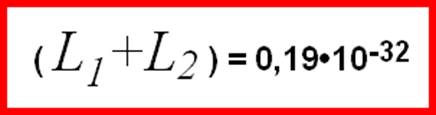The solution of these equations is (with allowance for (1-51)):

(1-61)

   This is how the elastic properties of the Gukuum, the neutron mass and the Planck constant are related to each other! Planck's constant determines the elastic properties of Gukuum (gukuum in traditional physics). And vice versa.
    From (1-61) follows a numerical evaluation of the elastic properties of the Gukuum:

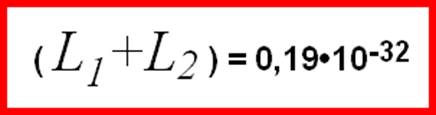
(1-62)

(in the GHS system).
The following is an estimate of the density of the Gukuum. In accordance with the laws of elasticity:

(1-63)

Or in units of the GHS system:

(1-64)

   ρ is the density of the gukuum. This is only the upper estimate of the density of the Gukuum, and the lower one can be equal to zero. Analysis is still being postponed.
   As is clear from formulas (1-62) and (1-63), the elasticity and density of Gukuum prove to be negligible in comparison with any terrestrial matter. At first glance it is a paradox. Insignificant in the density and elasticity of the carrier, but transfers enormous energies. Is it possible that the elastic parameters of the object formed by the fluctuation of the Gukuum are tens of orders higher than the elastic characteristics of the carrier itself? This is shocking. Compared with terrestrial substances. Here is the elastic substance: steel. For steel L₁≈L₂≈10⁶; ρ_steel≈10¹; and

 (1-65)

   That is due to what the speed of light is many times greater than the speed of sound in steel. So what is more "resilient", 10²¹ or 10⁵ ?! That's where it really is. What vortexes of ether can give the same ratio?
   It remains to be seen what each of the two Lame coefficients for Gukuum is equal to. You can make an assessment. For steel L₁≈L₂. If this is true for Gukuum, then

(1-66)

   (in the GHS system)
   But why should it be L₁≈L₂? And suddenly L₁>>L₂? That is, Gukuum is easy to shift, but is very heavy on compression? What if it's a LIQUID? It should be remembered that even if gukuum = liquid, then we are not talking about motions and vortices of a liquid, but about elastic waves in a liquid. But this assumption does not hold water. Light on all known experimental results is a transverse wave. This is the direction of the vectors of the electric and magnetic fields in electromagnetic waves. And transverse waves are possible only in a solid. Liquids, gases and ethers allow only longitudinal waves, compression waves.
  It is entirely possible that Gukuum is incompressible, as suggested in [25]. Formulas still allow this possibility. In this version there are no estimates for the density of Gukuum.
   So, Gukuum was the easiest as an ether. But it is elastic both in relation to compression, and to a shift (torsion) and capable of transferring through its oscillations colossal energies. If there was no elasticity to the shift, there would be no light. There would be no elementary particles.
   I want to note the special moments of the new theory.
   First, what was just mentioned: it is possible that the Gukuum is absolutely incompressible and all objects observed by man are only a game of stresses. It may well be that our reality is virtual! This is the first game of zeros - zeros of deformation.
   Secondly, it turns out that this virtuality does not end there. The discovery of the "winding" law introduces a special functional factor 1/r² into the integral in the calculation of energy. Without this factor, the energy integral of the "single loop" does not converge. That is, how small the constant C_j is in solution (1-2), the energy integral is still infinitely large in amplitude. So this constant is physically zero! That is, a single localized wave, one of its turns, has a zero amplitude! Another virtual reality. Another game of zeros! It turns out that everything in the universe is a game of zeros.
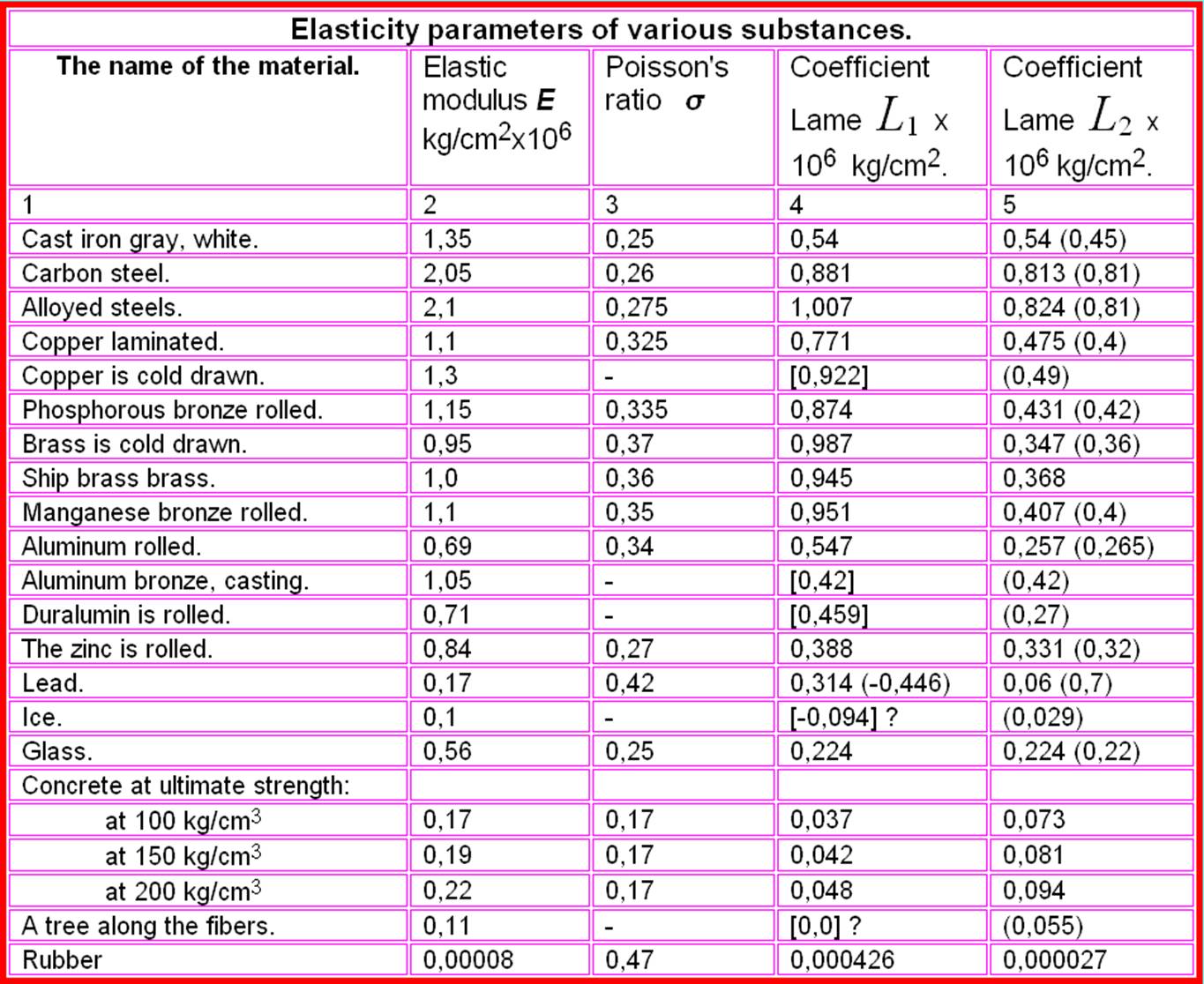
    2007.01.05. Addition. In order to establish the relationship between L₁ and L₂, it has been suggested that this ratio should somehow correlate with analogous relations in solid material substances. We have already mentioned the substance - steel, but I want more persuasiveness. We took the table of elastic properties from [39]. Something is there, something we have calculated up to the formulas from the theory of elasticity.
   The elastic modulus E, Poisson's ratio σ and the Lame coefficients L₁ and L₂ for various material substances. Based on materials from [39].
    In the calculations we used the elasticity formulas:

   Note. 1) Most of the values in columns 4 and 5 are calculated from the data from columns 2 and 3. No parentheses are used.
   2) The values in the columns in square brackets are calculated based on the elasticity formulas from the experimental data from the other columns except 2 and 3.
   3) In the parentheses - the corresponding experimental data.
    Conclusions. 1. The closeness of the values in columns 4 and 5 is seen with sufficient conviction. This may serve as some confirmation that in Gukuum L₁≈L₂. Provided that the original assumption is correct. For which we can not vouch.
2. There is an assumption that the universe is arranged in such a way that there are no fixed numerical constants in the universe. There are only mutual relations between physical quantities and parameters, expressed through other physical relationships and parameters. At the heart of everything lies the wave equation (which is simply an expression of the law of continuity and elasticity of the continuum of the universe). And the three Lame coefficients of this elasticity of the Gukuum and all physical quantities (elementary particle masses, fields, particle charges, Planck's constant, gravitation constant, etc.) are simply related by certain formulas and have no binding to any absolute numerical values. In other words, all visible physics and the universe are nothing more than a game, the interference of infinitesimal perturbations of the continuum. At the same time, our Universe is unambiguous, and there are no parallel universes.