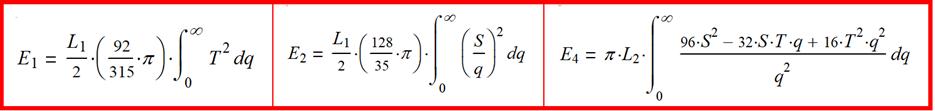1. Вселенная представляет собой твёрдый упругий континуум. Этот континуум
не имеет никаких числовых параметров или ограничений. Этот континуум, возможно, не имеет никакой массы или плотности. Но в силу закона сохранения, имеет некоторую сопротивляемость деформациям.
2. В этом континууме ВСЕГДА существовали и ВСЕГДА будут существовать все виды волн. Движение волн и создаёт всю картину вселенной, которую мы наблюдаем. В том числе волновые вихри создают материальные частицы. Математические описание прилагается.
3. Все видимые и невидимые объекты вселенной, от больших до маленьких, являются волновыми объектами в этом континууме. Все видимые и невидимые объекты вселенной, от больших до маленьких, являются решениями волнового уравнения:

(1-1)

4. Все волновые объекты в гукууме описываются алгебраическим заданием
параметров упругости твёрдого тела и трёхмерным волновым уравнением. При
этом просто предполагается, что это "малые" и "линейные" волны. Все вопросы типа «из чего состоит» не имеют смысла. Континуум и всё.

5. В качестве физических = буквенных параметров удобно использовать коэффициенты Ламэ L₁, L₂, L₃ (это элементарные комбинации из коэффициентов сжатия, сдвига и кручения твёрдого тела). Никаких числовых ограничений на коэффициенты Ламэ не накладывается. Просто коэффициенты Ламэ L₁, L₂, L₃ и всё.
6. Таким образом вселенная и вся содержащаяся в ней материя описываются только буквами, алгеброй. Однако между собой объекты могут сравниваться численно. Например массу волнового вихря протона можно численно сравнить с массой волнового вихря электрона.
7. Все элементарные частицы, поля, фотоны, шаровые молнии, чёточные молнии, тёмная материя - это различные виды решений волнового уравнения. Пока мы знаем несколько видов решений волнового уравнения, три сферических и три цилиндрических, но возможно этим вселенная не ограничивается.
8. Нелинейность, которая существует во вселеннной объясняется законом «наматывания линейного решения само на себя». Это очень важный закон, позволяющий понять образование элементарных частиц. В результате такого наматывания, или наслоения, линейное решение становится нелинейным и создаёт всё многообразие материального мира. Этот закон состоит в том, что в интеграл для энергии добавляется множитель  1/r². 

 

2. Вычисление энергии локов.

   Далее везде, как и в первой части, работаем в сферических координатах.

   Итак, мы берём мысленно волновой вихрь = лок, и располагаем его так, чтобы вращение волны происходило вокруг оси Z. Мы делаем предположение, что все колебания в локе происходят в одном и том же направлении. Так это или нет мы пока не знаем. Но это предположение близко к истине. Оно верно в первой степени приближения. Это наша математическая модель. Мы располагаем лок таким образом, чтобы эти колебания в локе происходили вдоль оси Z, а сама волна бежала вокруг оси Z. Точно так же бежит вокруг оси Z и энергия лока. И точно так же движение энергии лока создаёт угловой момент = спин.

Рис.1.

На Рис.1 показан фрагмент бегущей вокруг оси Z волны. Колебания в ней направлены вдоль оси Z. А волна бежит вокруг оси Z. Как будет видно из дальнейшего, несущая частота (синим цветом) постоянна на всём волновом вире. Однако с расстоянием от оси Z меняется амплитуда бегущей волны. Кроме того с расстоянием от оси Z меняется угловая скорость волны. То есть внешние слои отстают от внутренних.

   Частное решение волнового уравнения, сферические стоячие волны:

(1-2)

   Эта формула получена из линейной комбинации двух решений с разными Ф_m(φ).

   i,j,m - целые числа.  i=1,2,3.  j=0,1,2…  m=0,1,…,j;

   J_j(k•r) - Сферические функции Бесселя первого рода;

   Y_j(θ,φ) - сферическая поверхностная гармоника;
   Y_j(θ,φ)=P_jm(cosθ)•Ф_m(φ);
   Ф_m(φ)=sin(m•φ-k•c•t);

   P_jm(cosθ) - присоединенная функция Лежандра 1 типа, порядка  m  и ранга  j:

(1-3)

   В формулах многократно встречается величина k. Она связана только с реальной массой (энергией) частицы, ею и определяется. Это связующее звено между  ω  в колебательной части решения и радиальной координатой в функции Бесселя:  ω=k•c,  c - скорость света. На Рис. (1-1)  ω=k•c – это частота синей синусоиды, «несущей» волновой частоты. Также  k=1/λ , где  λ – приблизительный размер волнового вихря. Физика такова,что в каждой частице (в каждом решении) в силу физических причин устанавливается своя частота бегущей по кругу волны и свой размер частицы. Физические причины определяются формой решения, и тем как происходит наматывание решения само на себя, и как вся система стабилизируется в устойчивое состояние. Также у частиц бывают возбуждённые состояния. Исследовать это- дело будущего. Это можно только наблюдать. Таким образом все дальнейшие решения и формулы являются иллюстрацией того реального состояния,в котором находятся все волновые вихри =локи =элементарные частицы.

   Поскольку наш лок поставлен вертикально, то имеют место следующие соотношения. В решении для вектора смещения  W  имеется только одна компонента  W_Z .  W_x  и  W_y  равны нулю.

Имеем:

(1-4-1)

Имеют место следующие формулы перехода между декартовыми и сферическими координатами:

(1-4-2)

Таким образом:

(1-5)

Далее мы для простоты переходим к безразмерной длине:

(1-6)

Мы проверили, что все локи с j=2 имеют теоретическую бесконечность при вычислении энергий. Поэтому мы пропустили эти локи.

Согласно математическим справочникам, имеем формулу для смещения  W_Z  для первых четырёх локов (3,0), (3,1), (3,2) и (3,3):

(1-7)

Полезные формулы:

(1-8)

Далее выписываем формулы для смещений в сферических координатах:

(1-9)

Имеем формулы для тензора деформаций в сферических координатах:

(1-10)

Полная энергия лока после всех упрощений выражается формулой:

(1-11)

Далее вычисляем элементы тензора деформаций и энергии для каждого лока по отдельности.

Лок (3,0).

Для него не нулевыми оказываются три члена:

(1-12)

Энергия лока (3,0). Здесь квадрат тензора деформации интегрируется по пространству. В элементе объёма содержится множитель  q² , но в законе наматывания решения содержится  1/q². Эти сомножители взаимно уничтожаются и упрощают интеграл.

(1-13)

После подстановки значения W_i,j по формуле (1-12), получаем три не нулевых интеграла:

(1-14)

Оказывается, что все интегралы берутся и равны:

(1-15)

Лок (3,0) имеет осевую симметрию. Это видно по формуле для смещения (1-12), в ней нет угловых координат φ. График радиального распределения энергии и плотности энергии имеет вид:

Рис.2.

Как видно из графика, лок (3,0) имеет классическое уплотнение в центре.

Лок (3,1).

Отметим, что здесь  q  совсем другое, чем для лока (3,0).

Не равные нулю элементы тензора деформаций:

(1-16)

Энергия лока (3,1). Здесь квадрат тензора деформации интегрируется по пространству. В элементе объёма содержится множитель  q² , но в законе наматывания решения содержится  1/q². Эти сомножители взаимно уничтожаются и упрощают интеграл.

(1-17)

После подстановки значения W_i,j по формуле (1-12), получаем три не нулевых интеграла:

(1-18)

Оказывается, что все интегралы берутся и равны:

(1-19)

Лок (3,1) не имеет осевую симметрию. Это видно по формуле для смещения (1-16), в ней есть угловая координата φ. График радиального распределения энергии и плотности энергии имеет вид:

Рис.3.

Как видно из графика, лок (3,1) также имеет классическое уплотнение в центре.

Лок (3,2).

Отметим, что здесь  q  то же другое, чем для локов (3,0) и (3,1).

Не равные нулю элементы тензора деформаций:

(1-20)

Энергия лока (3,2). Здесь квадрат тензора деформации интегрируется по пространству. В элементе объёма содержится множитель  q² , но в законе наматывания решения содержится  1/q². Эти сомножители взаимно уничтожаются и упрощают интеграл.

(1-21)

После подстановки значения W_i,j по формуле (1-20), получаем пять не нулевых интегралов:

(1-22)

Оказывается, что все интегралы берутся и равны:

(1-23)

Лок (3,2) не имеет осевую симметрию. Это видно по формуле для смещения (1-20), в ней есть угловая координата φ. График радиального распределения энергии и плотности энергии имеет вид:

Рис.4.

Как видно из графика, лок (3,2) также имеет классическое уплотнение в центре.

Лок (3,3).

Отметим, что здесь  q  то же другое, чем для локов (3,0), (3,1), (3,2).

Не равные нулю элементы тензора деформаций:

(1-24)

Энергия лока (3,3). Здесь квадрат тензора деформации интегрируется по пространству. В элементе объёма содержится множитель  q² , но в законе наматывания решения содержится  1/q². Эти сомножители взаимно уничтожаются и упрощают интеграл.

(1-25)

После подстановки значения W_i,j по формуле (1-20), получаем пять не нулевых интегралов:

(1-26)

Все интегралы берутся и равны:

(1-27)

Лок (3,3) не имеет осевую симметрию. Это видно по формуле для смещения (1-24), в ней есть угловая координата φ. График радиального распределения энергии и плотности энергии имеет вид:

Рис.5.

Как видно из графика, лок (3,3) также имеет классическое уплотнение в центре.

   Итак, конечной энергией обладают также локи (3,0), (3,1), (3,2), (3,3), а также лок (5,0). Большие значения целочисленных аргументов создают серьёзные компьютерные проблемы. Локи (2,0), (2,1), (2,2) и все локи (4,0), (4,1), (4,2), (4,3), (4,4) имеют уходящие в бесконечность интегралы по энергии. Конечно, это не означает физическую бессмысленность этих локов. Просто это означает, что данное решение физически не устойчиво и уползает в некоторые другие решения, описываемые другими решениями (не сферическими) волнового уравнения.

Назад    Главная страница     Оглавление     Далее  

Страница размещена на сайте в мае 2005 года

--- ---