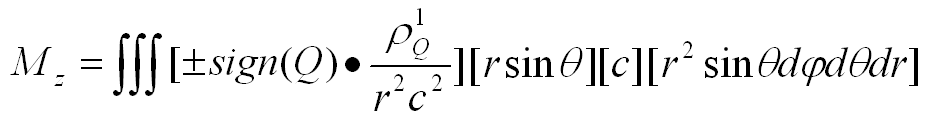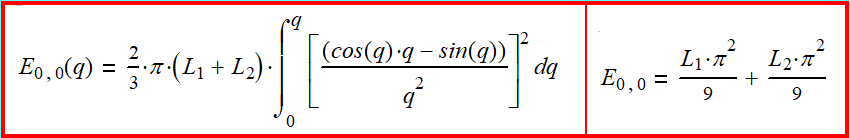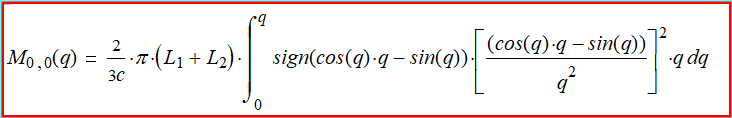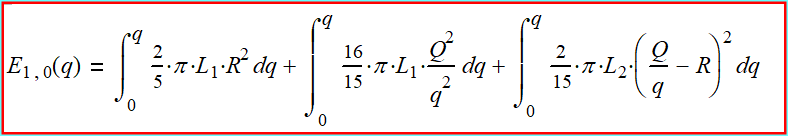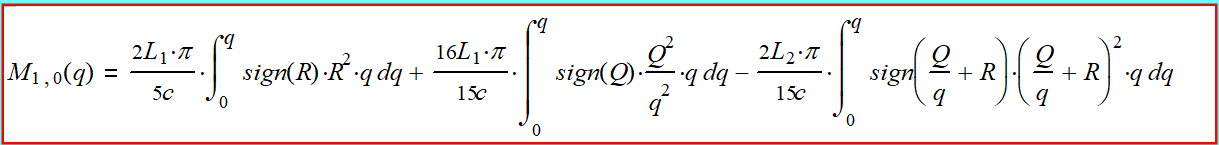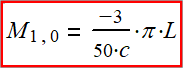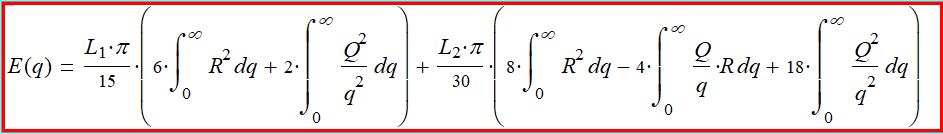Опубликовано: https://www.academia.edu/34522333/The_angular_momentum_of_the_lok

Уточнение: https://www.academia.edu/35952051/Angular_moments_spins_of_wave_vortices_loks_._Refinements

http://vixra.org/abs/1802.0239

1. Сущность гипотезы.

   Наша математическая модель состоит в том, что:

1. Вселенная представляет собой твёрдый упругий континуум. Этот континуум
не имеет никаких числовых параметров или ограничений. Этот континуум, возможно, не имеет никакой массы или плотности. Но в силу закона сохранения, имеет некоторую сопротивляемость деформациям.
2. В этом континууме ВСЕГДА существовали, и ВСЕГДА будут существовать все виды волн. Движение волн и создаёт всю картину вселенной, которую мы наблюдаем. В том числе волновые вихри создают материальные частицы. Математические описания прилагаются.
3. Все видимые и невидимые объекты вселенной, от больших до маленьких, являются волновыми объектами в этом континууме. Все видимые и невидимые объекты вселенной, от больших до маленьких, являются решениями волнового уравнения: 

(1-1)

4. Все волновые объекты в гукууме описываются алгебраическим заданием
параметров упругости твёрдого тела и трёхмерным волновым уравнением. При
этом просто предполагается, что это "малые" и "линейные" волны. Все вопросы типа «из чего состоит» не имеют смысла. Континуум и всё.

5. В качестве физических = буквенных параметров удобно использовать коэффициенты Ламэ L₁, L₂, L₃ (это элементарные комбинации из коэффициентов сжатия, сдвига и кручения твёрдого тела). Никаких числовых ограничений на коэффициенты Ламэ не накладывается. Просто коэффициенты Ламэ L₁, L₂, L₃ и всё.
6. Таким образом, вселенная и вся содержащаяся в ней материя описываются только буквами, алгеброй. Однако между собой объекты могут сравниваться численно. Например, массу волнового вихря протона можно численно сравнить с массой волнового вихря электрона.
7. Все элементарные частицы, поля, фотоны, шаровые молнии, чёточные молнии, тёмная материя - это различные виды решений волнового уравнения. Пока мы знаем несколько видов решений волнового уравнения, три сферических и три цилиндрических, но возможно этим вселенная не ограничивается.
8. Нелинейность, которая существует во вселенной, объясняется законом «наматывания линейного решения само на себя». Это очень важный закон, позволяющий понять образование элементарных частиц. В результате такого наматывания, или наслоения, линейное решение становится нелинейным и создаёт всё многообразие материального мира. Этот закон состоит в том, что в интеграл для энергии добавляется множитель  1/r². 

 

2. Вычисление угловых моментов (спинов) локов.

   Далее везде мы работаем в сферических координатах.

   Итак, мы берём мысленно волновой вихрь = лок, и располагаем его так, чтобы вращение волны происходило вокруг оси Z. Мы делаем предположение, что все колебания в локе происходят в одном и том же направлении. Так это или нет, мы пока не знаем. Но это предположение близко к истине. Оно верно в первой степени приближения. Это наша математическая модель. Мы располагаем лок таким образом, чтобы эти колебания в локе происходили вдоль оси Z, а сама волна бежала вокруг оси Z. Точно так же бежит вокруг оси Z и энергия лока. И точно так же движение энергии лока создаёт угловой момент = спин. 

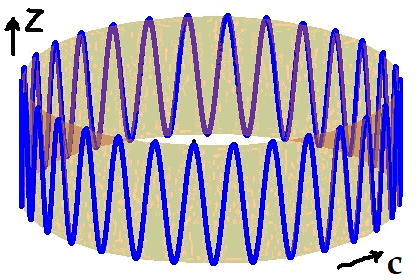
Рис.1.

На Рис.1 показан фрагмент бегущей вокруг оси Z волны. Колебания в ней направлены вдоль оси Z. А волна бежит вокруг оси Z. Как будет видно из дальнейшего, несущая частота (синим цветом) постоянна на всём волновом вире. Однако с расстоянием от оси Z меняется амплитуда бегущей волны. Кроме того, с расстоянием от оси Z меняется угловая скорость волны. То есть внешние слои отстают от внутренних слоёв.

   Далее используем материалы, изложенные в предыдущей статье.

Мы для простоты переходим к безразмерной длине: 

(2-1)

Полезные формулы: 

(2-2)

   Эвристическое предположение.
   Для вычисления углового момента необходимо проинтегрировать угловые моменты всех бесконечно малых элементов волнового вихря. Было сделано эвристическое предположение: знак функций  Q  и  R  , стоящих в квадратичных формах для энергии локов как раз и определяет направление движения этого элемента энергии. Это достаточно логичное, и достаточно непротиворечивое предположение. Анализ формул для энергий локов, анализ формул для  R  и  Q , отсутствие в них угловой зависимости от  φ , показывает, что в этом случае энергия в локах вращается как бы сферическими слоями вокруг оси  Z .  В определении направления движения слоев массы = энергии простых локов (0,0) и (1,0) участвует только одна переменная  q . При переходе из слоя в слой направление движения энергии может даже изменяться на противоположное. Но если перемену знака зафиксировать можно, то сам знак или направление движения элемента хотя бы в одном слое пока определить не представляется возможным. Поэтому все приводимые ниже формулы справедливы "с точностью до наоборот".
   Таким образом, правдоподобная общая формула для момента импульса простейшего лока  M_z , имеет вид: 

(2-3)

ρ¹ плотность энергии элемента объёма.
ρ¹_Q - часть плотности энергии зависящая от Q.
Q - ранее определённая вспомогательная величина.
   Под знаком интеграла четыре элемента, которые для наглядности выделены в квадратные скобки. Первая квадратная скобка содержит в себе элементы плотности массы лока (отличие от энергии - c² в знаменателе), с учетом "наслоения" ( r² в знаменателе) и также с учетом знака, с которым эта масса войдет в формулу момента импульса (функция sign). То есть, в зависимости от направления вращения данного элемента. Вторая квадратная скобка - расстояние от оси вращения - оси  Z . Третья квадратная скобка - скорость движения элемента массы, скорость света. Четвертая - элемент объема. То есть это момент импульса в классическом его понимании.
   Подынтегральное выражение может содержать несколько функциональных зависимостей, в зависимости от сложности лока  (m,n). 

Лок (0,0).

Энергия лока (0,0). Общая формула энергии: 

(2-4)

Общее уравнение для углового момента, согласно формуле (2-3): 

(2-5)

Распределение углового момента и распределение плотности углового момента внутри частицы в зависимости от радиуса иллюстрируем по поведению интеграла и подинтегрального выражения в формуле (2-5):

Рис.2.

Как видно из графика, плотность спина на бесконечности стремится к нулю, а сам момент асимптотически приближается к некоторой величине, равной примерно: 

(2-6)

Лок (1,0).

Энергия лока (1,0). Общая формула энергии: 

(2-7)

Как видно из формулы (2-7) в локе (1,0) как бы три функциональных «ядра» образования спина. Это  Q , R. Кроме того, функция  sign  содержит угловую координату  θ.  Общее уравнение для углового момента, согласно формуле (2-3): 

(2-8)

Если предположить, что  L₁=L₂=L , что в большинстве справедливо для всех земных материалов, то получаем следующие графические зависимости радиального распределения углового момента и плотности распределения углового момента внутри частицы в зависимости от радиуса. Без корректировочных коэффициентов:

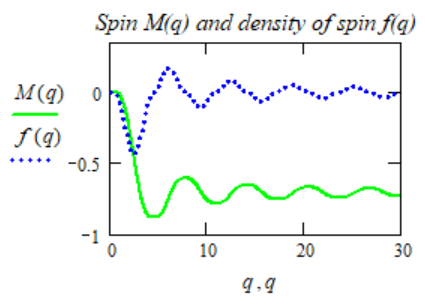
Рис.3.

Как видно из графика, плотность спина на бесконечности стремится к нулю, а сам момент асимптотически приближается к некоторой величине, равной примерно: 

(2-9) 

Лок (1,1).

Энергия лока (1,1). Общая формула энергии: 

(2-10)

Как видно из формулы (2-10) в локе (1,1) тоже три «ядра» образования спина. Но они сводятся к тем же самым трём: это  Q , R  и  Q•R.  Кроме того, функция  sign  содержит угловые координаты  θ  и  φ. Тройной интеграл с функциями sign внутри очень сложен, поэтому нет полной уверенности, что мы всё сделали правильно. Общее уравнение для углового момента, после интегрирования по угловым координатам, согласно формуле (2-3): 

(2-11)

Следует обратить внимание, что коэффициенты в формуле для энергии и в формуле для момента значительно отличаются. Это связано с тем, что в локе (1,1) появляются зависимости от угловых координат. Которые после довольно сложного интегрирования (из-за присутствия функции sign ) приводят к таким коэффициентам.

Если предположить, что  L₁=L₂=L , что в большинстве справедливо для всех земных материалов, то получаем следующие графические зависимости радиального распределения углового момента и плотности распределения углового момента внутри частицы в зависимости от радиуса. Поправочный коэффициент, чтобы были наглядны оба графика, для  M  равен 0,2.

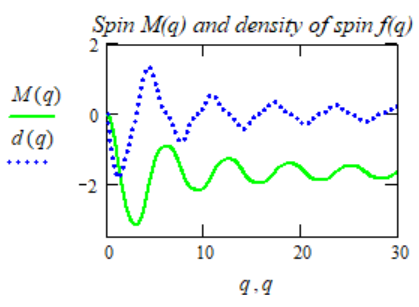
(2-12)

Как видно из графика, плотность спина на бесконечности стремится к нулю, а сам момент асимптотически приближается к 0,3. С учётом всех коэффициентов, принятого на графиках масштаба, момент лока (1,1) равен примерно: 

(2-13)

Сравнивать угловые моменты (спины) локов не имеет особого смысла. Потому что в решениях присутствуют постоянные коэффициенты, разные для всех решений. Но участие молодых и сильных математиков и физиков позволит внести ясность в проблему идентификации между реальными частицами и локами.
   Однако уже сейчас можно сделать предварительные выводы от проделанной работы.
1. Выбранные величины  R  и  Q для определения знака элемента спина оказались достаточно удачными. Если посмотреть на окончательные формулы для спинов (2-6), (2-9) и (2-13), то видно, что спины у протона и электрона получились противоположных знаков, что соответствует реальности. Спин нейтрона получился пренебрежимо малым по сравнению со спинами электрона и протона, что тоже соответствует реальности. И расхождение по абсолютной величине между спинами электрона и протона всего в два раза, что тоже можно считать удачей.
2. Вместе с этим таки появляются сомнения, что мы учли все тонкости объектов и происходящих в них процессов, что привело к разнице в абсолютной величине спинов электрона и протона в два раза. Конечно, это очень хорошо. Если бы мы совершали далёкие от реальности выкладки, то разница могла быть на многие порядки. Например, существуют множество теоретических уточнений к изначальному волновому уравнению (1-1), которые могут привести к вариациям решений.
3. В силу удачности нашего выбора функций  R  и  Q , возможно их дальнейшее применение для вычисления зарядов локов. Это будет проделано абсолютно аналогично моменту. А общность заряда и момента вращения отмечалась нами и ранее.
4. Необходимо искать более удачные функции  R  и  Q , которые дали бы ещё более точные соответствия между спинами электрона и протона. А также и нейтрона.

Другие локи.

   Как показывает наша проверка, локи (3,1), (3,2) и (3,3) также имеют конечные, вычисляемые угловые моменты. Поэтому идентификация элементарных частиц пока ещё затруднена. Также мы не можем утверждать, что имея спины локов по формулам (2-6), (2-9), (2-13), мы можем их сравнивать между собой. Эти формулы получены в предположении, что  q=k•r , а коэффициенты  k  связаны с реальными массами частиц. Эти массы разные. Кроме того, в каждом решении возможна константа в начале, которая традиционно определяется только на основе реальных масс и спинов. Других соображений у нас пока нет. Поэтому мы пока откладываем идентификацию элементарных частиц. Мы предполагаем, что лок (1,0) – нейтрон, а лок (1,1) – протон. На основании похожести графиков распределения зарядов внутри нейтрона и спина внутри лока (1,0).

Назад    Главная страница     Оглавление     Далее  

--- ---