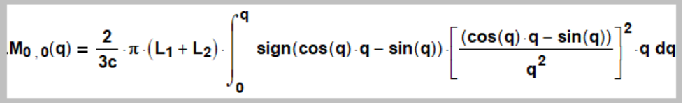|
Назад Главная страница Оглавление Далее ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И СПИН. ВНИЗУ ИЗЛОЖЕНО ДОПОЛНЕНИЕ ОТ 12.04.2019. Опубликовано: https://www.academia.edu/34532615/Electric_charge_and_spin_of_elementary_particles Ниже использована информация и графики о "структуре нуклонов" из
того же справочника Яворского - Детлафа [10]. -------------------- В
традиционной физике для иллюстрации взаимодействия между
частицами вводится понятие электрического заряда. Читатели
настолько привыкли к этому понятию, к удобству работы с этим
понятием, что воспринимают его как объективную реальность.
То есть все считают, что электрическое поле, как и
магнитное, как и гравитационное, как и собственно материя,
элементарные частицы - всё это реально существует. А как же
иначе? Всё это воспринимается либо нашими органами чувств,
либо приборами, сконструированными под наши органы чувств.
Даже придуман бозон, аналогичный бозону Хиггса, которые
носитель заряда.
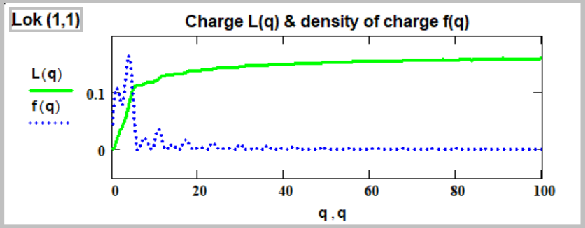
Это - рисунок нейтрона. С точной формулой.
Нейтрон состоит из концентрических волновых сфер, вращающихся вокруг
вертикальной (на данном рисунке) оси Z .
На рисунке: портрет электрона
(приблизительный) и формула для него (абсолютно точная). Причём ни одно из
волновых колец, составляющих тело электрона не может быть удалено или отделено.
Нет такой силищи в природе! И что самое забавное: все эти кольца вращаются по
кольцу со скоростью света, но соседние кольца вращаются в противоположные
стороны. Амплитуда этих круговых волн в месте соприкосновения колец падает до
нуля. И это тоже не фантазмы, это строгая математика. Плюс подтверждённая
изложенными ниже сравнениями с экспериментом.
Оказывается, учёных эти вопросы интересовали
давным - давно. Эксперименты проводились в 60-70 годы, когда
о модели Упругой Вселенной никто ничего не знал и не
подозревал. Внутреннее устройство элементарных частиц было
абсолютной загадкой для всех. Помнится, и я в свои
студенческие годы (1971-1977, МФТИ) неоднократно
задумывался: ну как же они там внутри устроены? Что это за
твёрденький электрончик, который вращается вокруг
твёрденького протончика? Почему он вращается так устойчиво,
несмотря на все столкновения с окружающими электронами?!
Почему не падает на ядро атома? Откуда берутся квантовые
законы?
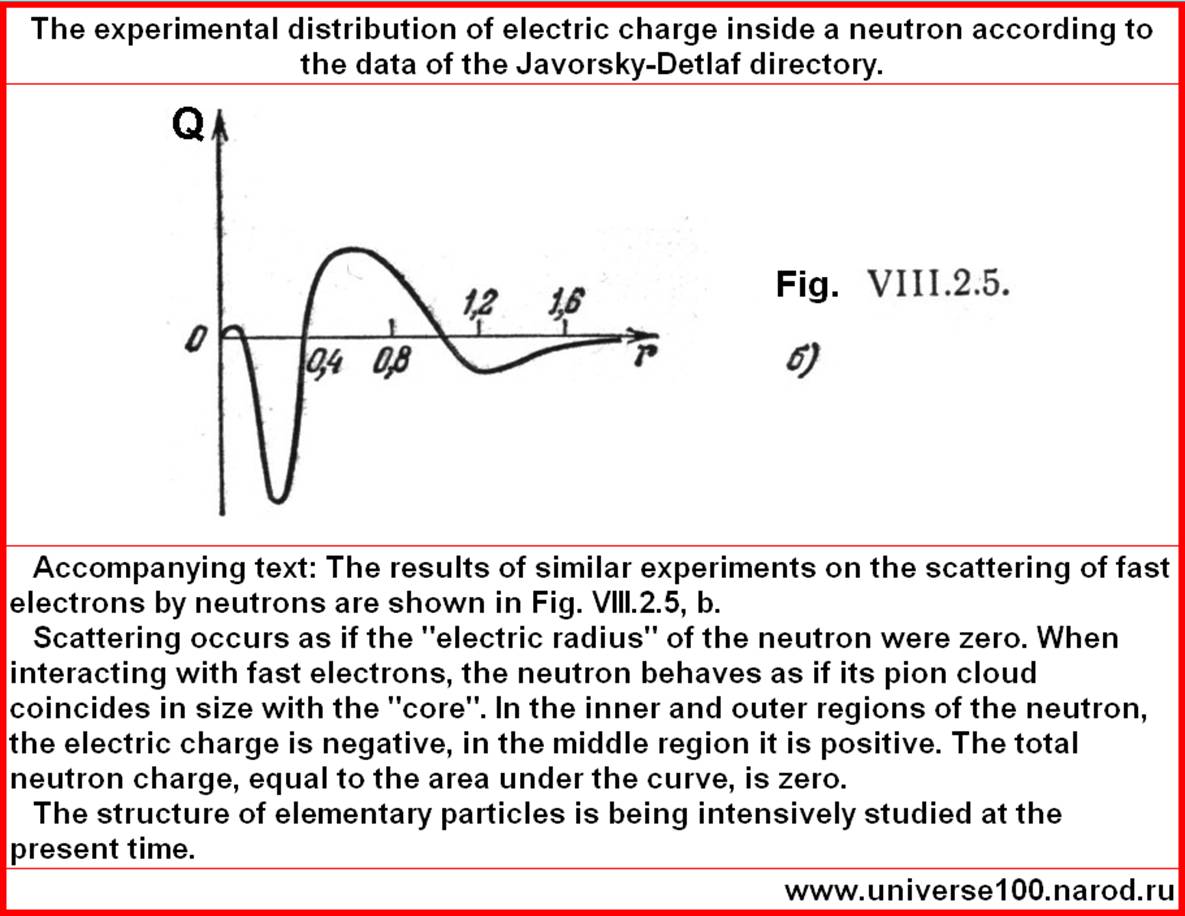
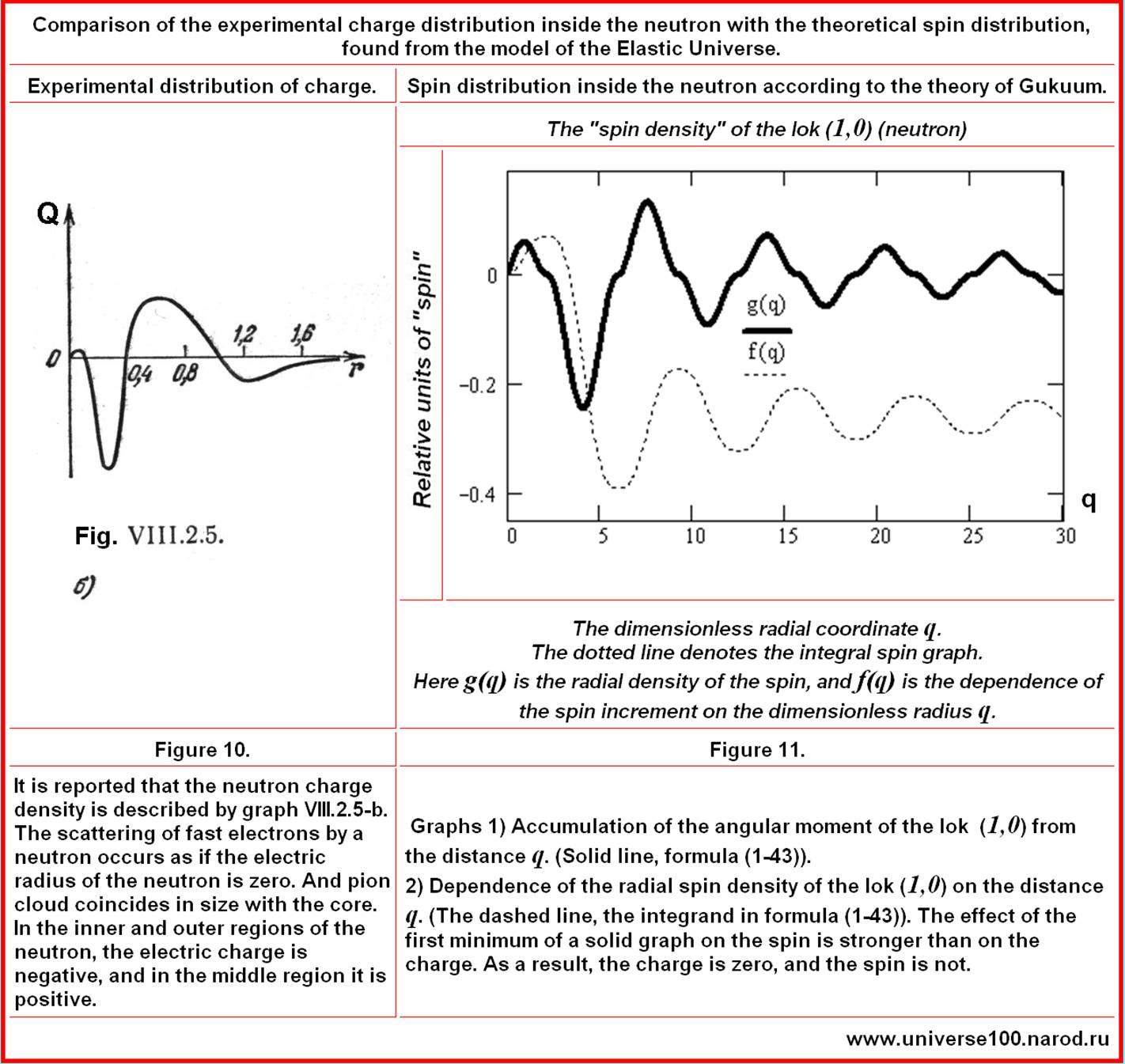
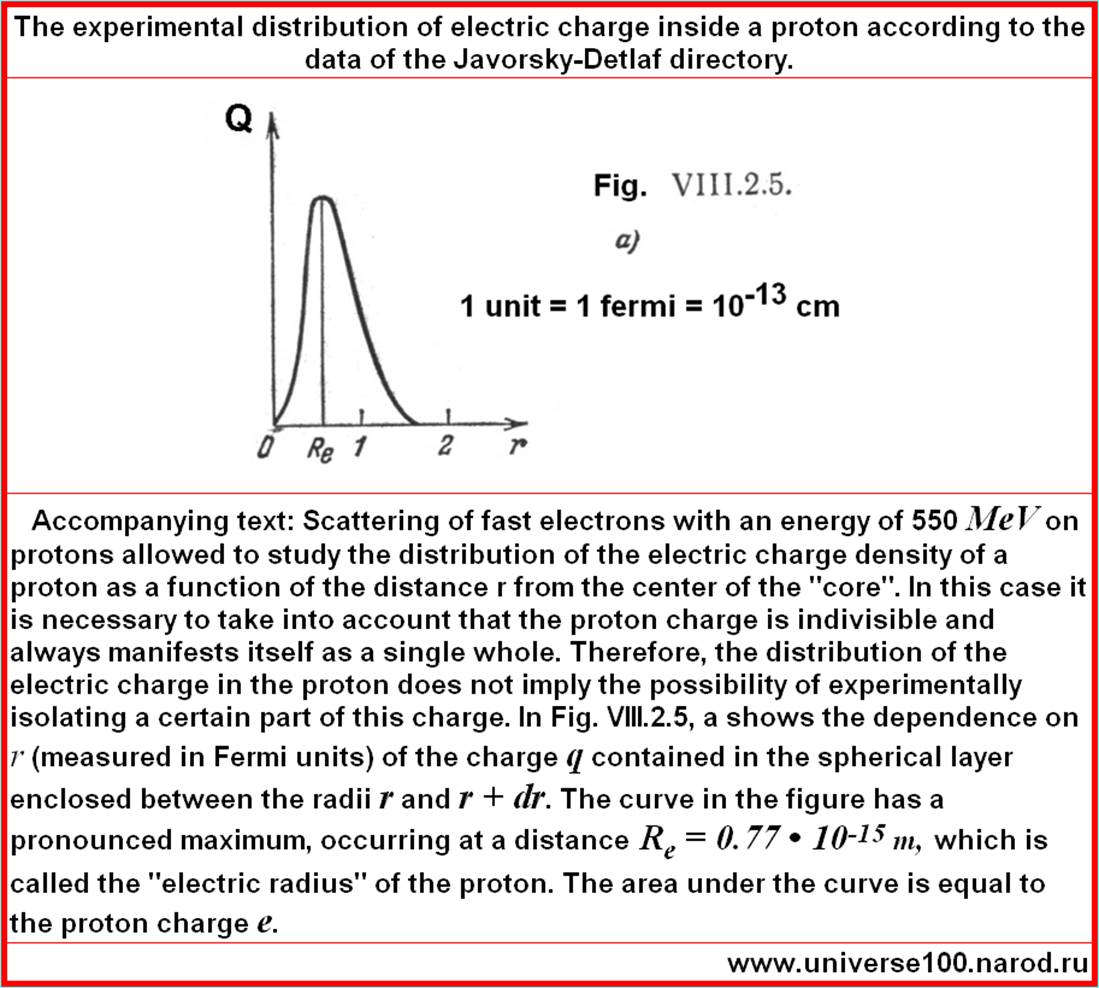
Сравнение имеющихся экспериментальных данных с имеющимися теоретическими результатами. Итак, для начала, первый рисунок - взят из справочника Яворского 1980 года. Он создан Яворским на базе тех самых результатов экспериментов 60-70-х. Это старые (но бесценные!) исследования о распределении заряда внутри протона и нейтрона.
Далее сравнение в таблице
ниже. Мы немного изменили первый рисунок по сравнению с
книгой, потому
что произошла накладка: на нём буквой q
обозначена плотность электрического заряда. А мы, того не подозревая, в своей
теории обозначали через q безразмерную радиальную
координату. Ну и ясно, кто-то запутается, поднимет шум, а обвинят во всем нас.
Поэтому плотность заряда здесь мы обозначили как Q.
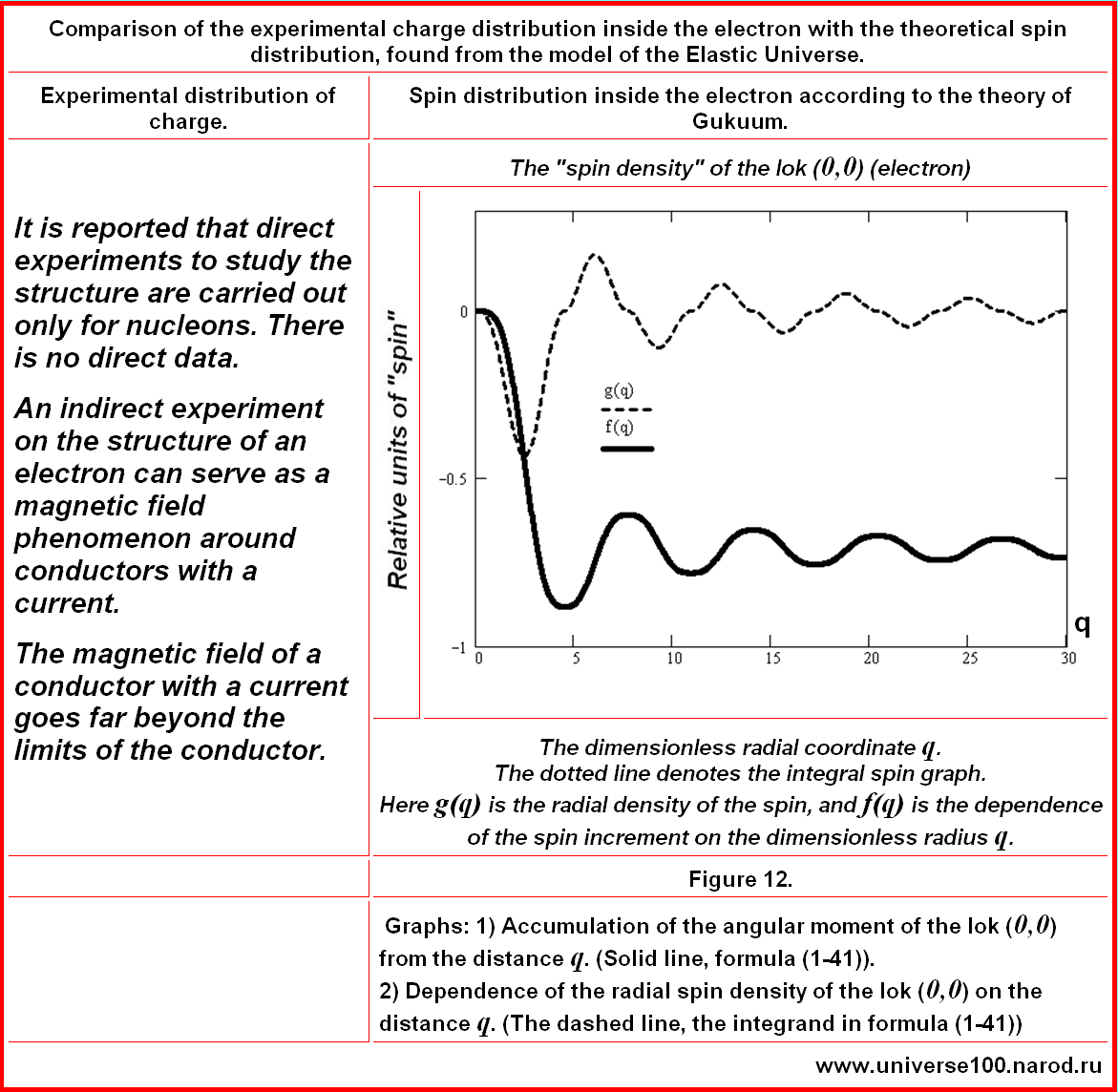
КОММЕНТАРИИ. Здесь,
на рисунке справа, жирной сплошной линией обозначена
радиальная плотность распределения спина внутри предполагаемого нейтрона. А
пунктиром - интегральная плотность спина в зависимости от расстояния.
(1-58) Превышение теории над экспериментом, в 2 раза. Но экспериментальные данные трактовались как бомбардировка нейтрона точечным электроном. А на самом деле электрон огромен… Может быть размеры электрона наложились на результаты всех экспериментов. Если не какая иная причина. ---------------------- А что мы имеем с протоном? Каковы распределения зарядов и спинов в
протоне и его теоретическом аналоге? - Ситуация здесь очень похожая.
Ниже на правом графике - наше теоретическое распределение спина внутри предполагаемого протона по теории Упругой Вселенной. Напомним, что согласно нашему пояснению, данному в начале этого сообщения, распределения спина и заряда внутри частиц должны коррелировать, потому что для вычисления этих величин нужно суммировать знакопеременные ряды, в них обязательно должна учитываться разнонаправленность движения сферических слоёв энергии внутри частиц.
КОММЕНТАРИИ. Здесь жирной сплошной линией обозначена
радиальная плотность распределения спина внутри предполагаемого протона. А
пунктиром - интегральная плотность спина в зависимости от расстояния.
Здесь и далее на графиках
справа величина ρM означает
"плотность момента импульса". График справа отвечает формуле (1-45).
Очевидна близость обеих графиков на правом рисунке с распределением
заряда слева. При этом нет уверенности в том, что под термином
"радиальная плотность" на рисунке слева имелось ввиду то же, что на
графике справа.
(1-57) Достаточно близко к эксперименту (0,77х10-13 см). Впрочем все ниже идущие близости эксперимента и теории не удивительны после того, как их конфигурации по плотности энергии совпали.
---------------------------
А что у нас с электроном?
--------------------------- Для приближённых оценок и экспериментов заряд элементарной частицы можно определять как
Q = k*S , (А)
где Q
- заряд, k - некоторый коэффициент
(который весьма вероятно может оказаться один и тот же для всех частиц), а
S
- спин частицы. Так, для протона и электрона это утверждение уже выполняется
с очевидностью. А вот для нейтрона по нашим данным остаётся предположение, что
нейтрон имеет небольшой спинчик и небольшой зарядик.
Q = k*S + F(r,θ,φ) + …, (Б)
- - <> - - ДОПОЛНЕНИЕ ОТ 12.04.2019.
Электрический заряд и электрическое поле элементарных частиц. Абстракт. Показана неточность современного воззрения на электрический заряд и электрическое поле. Вся теория Максвелла, Кулона и других гигантов физики, справедлива только для макромасштабов, порядка более 100 размеров элементарных частиц. В микромасштабе действуют совсем другие законы. В том числе поле одиночного заряда не имеет сферической симметрии и кулоновской зависимости обратной от радиуса. 1. Введение. Чем сильнее человечество углубляется в познание Природы, тем труднее двигаться. Сложнее становятся понятия и математические формулы. Тем ниже доверие учёных к опубликованным результатам. Теория Упругой Вселенной дала ответ на происхождение массы частиц, момента вращения частиц. Но в вопросе электрического заряда возникла задержка. Главным образом из-за недоверия учёных к нашей теории. Что брать за основные аксиомы? Учёные исходят из общепринятых постулатов. Если исходить из традиционной физики, то справедлив закон Гаусса:
То есть заряд равен интегралу от дивергенции электрического поля. Согласно уравнениям Максвелла:
А поскольку внутри волновых вихрей (локов) никаких зарядов нет, то у нас всегда будет получаться ноль. Что проверено нашими аналитическими выкладками. Это как бы обязательная процедура. Доверяй но проверяй. Мы исходили из уравнения:
Где A - электромагнитный векторный потенциал, полученный из нашей единой теории всех полей. Это всё мы давно нашли, опубликовано в наших предыдущих статьях. Далее W – смещение в гукууме. Как известно из математики, для любого векторного поля W существует такое разложение Гельмгольца:
что:
Согласно сделанным нами ранее выводам, A – это электромагнитный векторный потенциал, а G напряжённость гравитационного поля. Согласно учебнику Ландау - Лифшица
Но учитывая (5), можно написать:
Таким образом мы можем выразить заряд любого волнового вихря через смещения W которые мы ранее подсчитали и опубликовали 15 лет назад. Заряд выражается в виде интеграла по пространству-времени.
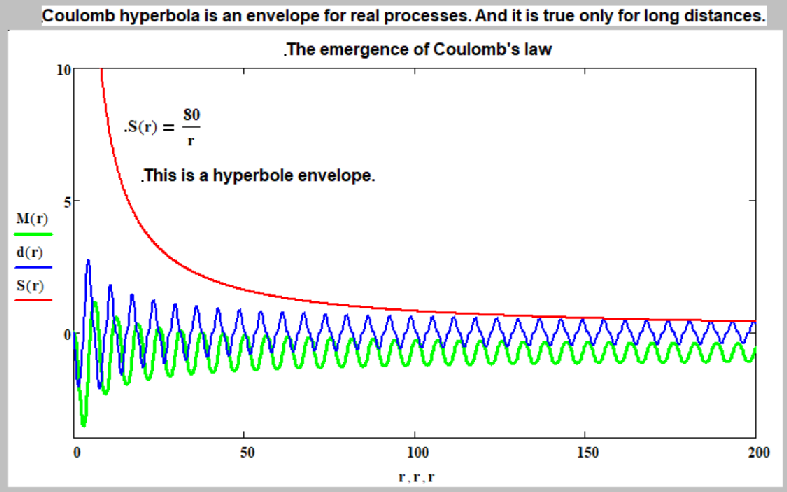
Мы проделали все выкладки для локов (0,0), (1,0) и (1,1). И как и ожидалось, везде получили ноль. q=0 (9) С моментом вращения частиц была аналогичная история. Момент вращения локов при формальном интегрировании тоже давал ноль. Однако после того как мы учли направление вращения элементов лока, то в результате появились не нулевые и имеющие смысл интегралы. Что означает такой результат? Он означает, что физики в настоящее время не знают, что такое заряд и что такое электрическое поле. За основу описания электрического поля и заряда взята простая, красивая, идеализированная математическая модель. Модель уравнений Максвелла, Кулона и Гаусса. В которой как бы (формула 2) заряд отдельно, а электрическое поле отдельно. История, которая закрепилась и получила продолжение с бозоном Хиггса, когда все элементарные частицы отдельно, а их массы отдельно, как гирьки в кармане, в виде бозона Хиггса. У нас давно возник вопрос. Физики ядерщики тратят миллиарды на исследование разрушения протонов. На релятивистские исследования. Но почему-то не исследуются взаимодействия между заряженными частицами на малых расстояниях. Почему? Да наверно исследуются, только об этом не шумят, потому что все законы в микромире нарушаются и начинают работать «волновые функции», «вероятность» и «принцип неопределённости», которые нарушают весь порядок. Как всё выглядит на самом деле? Кулоновская зависимость возникает как огибающая реальных процессов в волновом вихре. На больших расстояниях (порядка 100 единиц на графике) имеет место полное совпадение с реальностью. Но на малых расстояниях не работают ни закон Кулона, на законы Максвелла, ни формула Гаусса.
(10) Это заставило нас по новому подойти к расчёту и описанию электрического заряда и электрического поля. 2. Размерность заряда. Если мы сравним размерность спина и размерность заряда, то получаем. [Спин]: г1•см2•сек-1 . (11) [Заряд]: г1/2•см3/2•сек-1 . (12) То есть мы видим разницу в массовой составляющей и в линейной составляющей. Этот факт мы берём далее за основу поиска формул зарядов элементарных частиц. Если в наш интеграл для вычисления спина входила плотность энергии и радиальная координата в целом виде, то весьма вероятно, что в заряд эти величины должны входить в изменённом виде. В частности, весьма вероятно, что степень радиальной координаты под интегралом должна быть на ½ меньше. Это конечно не окончательный вывод. Ведь радиальная координата входит и в формулу энергии. С чем связано отличие размерностей спина и заряда? Как мы ранее констатировали, исходя из физических свойств, между спином и зарядом много общего. Согласно справочнику Яворского-Детлафа, близки экспериментальные графики их распределения внутри частиц. Близки знаки этих величин. И спин и заряд нейтрона равен нулю. При этом мы объяснили, почему такой маленький по массе электрон имеет такой большой спин и заряд. Это следствие больших размеров электрона, его большого волнового облака. В центре электрона плотность равна нулю, как у бублика. Протон же очень маленький и очень плотный, имеет уплотнение в центре «керн». То есть, сравнивая спины и заряды, мы делаем вывод, например для электрона, что в образование спина и заряда входят одни и те же элементы волнового вихря (0,0). Они входят с одинаковыми знаками, но для заряда эти элементы умножаются на некоторый функциональный коэффициент. Мы не будем гадать о точном виде этого коэффициента, потому что не представляем что там происходит на микроуровне. Это очень сложная задача для будущей молодёжи. Мы удовлетворимся некоторым приближением. Спины частиц не взаимодействуют на расстоянии, а заряды взаимодействуют. В этом важное различие между спинами и зарядами. Но так ли это? Почему мы так уверены, что при сближении двух протонов взаимодействуют заряды? Это же ни откуда не следует. С тем же успехом мы могли бы утверждать, что взаимодействуют спины. Мы не знаем процессов на микроуровне. Возможно, что взаимодействие электрона и протона начинается с того, что протон цепляет электрон какими-то своими элементами, заставляет его развернуться, и разворачивается сам. И только потом начинается взаимодействие. Наука не знает и не понимает этого. Это отнесено в область «волновые функции», «вероятность» и «принцип неопределённости». Взаимодействуют какие-то компоненты в тензорах деформаций волновых вихрей. То есть в тензорах смещений гукуума. Ну тензоры двух электронов как бы одинаковы и их взаимодействие вполне естественно и понятно. А вот взаимодействие тензоров электрона и протона требует поиска каких-то родственных компонент тензоров. Существование таких родственных компонент подтверждается и совпадением (с точностью до знака) спинов протона и электрона. Возможно направление поиска таких компонент. Попробуем сравнить формулы для энергии протона и электрона.
(13) Как видно, одинаковые элементы есть, это Q . При этом параметр k в формуле q=k*r в формулах для (0,0) и (1,1) разный, отличается на три порядка (примерно как масса протона отличается от массы электрона). Поэтому какой-то синхронности колебаний в волне (0,0) и (1,1) ожидать не приходится. Однако, поскольку интеграл по r берётся до бесконечности, может оказаться, что присутствие параметра k не играет роли. Таким образом весьма вероятно предположение, что во взаимодействии зарядов как раз играет параметр Q . Кроме того, справедлив такой вывод. Поскольку экспериментально установлено равенство (по абсолютной величине) спинов и зарядов протона и электрона, этот факт мы берём за основу. То есть и по формулам должно происходить то же самое. Это самое и происходит для спинов протона и электрона, но с некоторой погрешностью. Какую формулу и какой конечный результат вычисления спина считать более точными, для электрона или для протона? Формулы для протона весьма сложны, неоднозначны, и вызывают мало доверия. Поэтому лучше опираться на данные по электрону. Попробуем действовать методом подбора. 3. Взаимодействие зарядов. Согласно нашей теории Упругой Вселенной, элементарные частицы – это единые объекты. В них нет разделения: вот это частица, а вот это её гравитационное поле. По аналогии с планетой Земля, вот Земля, а вот её атмосфера. Или: вот это заряд частицы, а вот это её электрическое поле. В нашем понимании это чисто условное разделение. Точно так же когда-то учёные считали, что «все тела падают вниз». Но потом выяснили, что «низ» это тоже тело, Земля. И пришли к более общей формулировке, что «между всеми телами существует гравитационное притяжение». Поэтому мы выбираем новый путь. А именно, исходя из общих формул, полученных нами для волновых вихрей, мы попытаемся подобрать формулу электрического взаимодействия. Итак, мы ещё 15 лет назад получили интеграл, который мы назвали «интеграл энергии» волновых вихрей (локов). При этом мы использовали «закон наматывания». Этот интеграл мы составили, исходя из традиционных представлений физики, как сумму квадратов элементов тензора деформаций.
(14) Мы проделали все необходимые математические операции, и выяснили, что интегралы энергии для локов (0,0), (1,0) и (1,1) благополучно вычисляются. Далее мы составили интегралы, аналогичные вращательному моменту из традиционной физики.
Здесь ρM – плотность момента вращения в волновом вихре, вычисляемая по стандартным правилам, массу умножить на радиус вращения. Масса это энергия, делённая на с2. Энергия вычисляется по формуле (14). Всё эти кропотливые выкладки мы проделали с помощью Маткада, все интегралы сошлись и имеют довольно таки разумные значения. Маткад очень удобен, потому что формулы из него наглядны. Посмотрите формулу (15). А если бы мы здесь показали формулу из Мапле, то никто ничего бы не понял. Таким образом, исходя из внутреннего устройства волновых вихрей мы получили массы и спины элементарных частиц. Всё это сделано 15 лет назад и прекрасно согласуется с экспериментом. Мы получили некоторые интегральные формулы для волновых вихрей (14) и (15), которые, как оказалось имеют реальные проявления. Интеграл (14) проявляется в массе частиц. А интеграл (15) проявляется в моменте вращения (спине) частиц. Мы задаём вопрос: а есть ли ещё какие-то интегральные величины у волновых вихрей, кроме массы и момента вращения? Которые могли бы в реальности проявляться как некоторые физические свойства, кроме массы и спина? Например эти интегралы могли бы быть идентифицированы как электрическое поле, электрический заряд, и даже вообще какие-то новые свойства элементарных частиц. Как видно из определений и формул, момент вращения это по сути энергия, умноженная на радиус вращения. Ничего загадочного. Однако на практике такое простое умножение добавляет к массе частицы ещё одно физическое свойство: спин. А почему бы не попробовать другие комбинации? Нами ранее установлено, что во многом электрические свойства частиц коррелируют с их спинами. Из этих соображений мы делаем предположение, что искомый интеграл электрического заряда тесно связан с интегралом для спина. То есть, если интеграл для момента вращения вычисляется по формуле
То интеграл для электрического заряда может вычисляться по формуле:
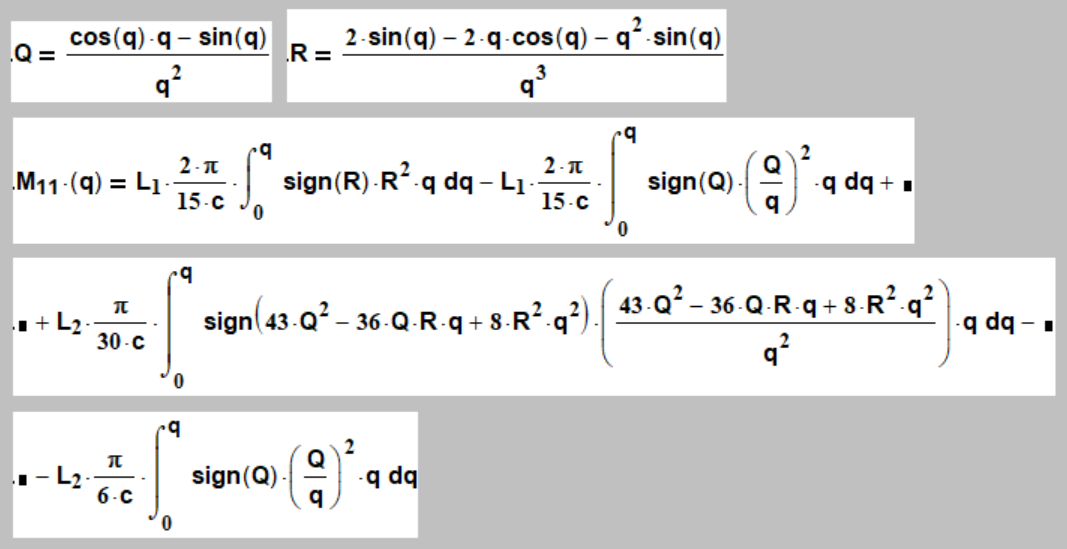
То есть с добавкой в подъинтегральное выражение rs , где s – некоторый ряд чисел, имеющих физический смысл. s=1, ½, -½, -1. Мы взяли такой ряд чисел потому, что ранее в изучении размерностей спина и заряда мы установили как раз отличие на r1/2 . А значения вне этой области будут давать расходящиеся интегралы. Мы вычислили интегралы (17) для всех трёх локов (0,0), (1,0) и (1,1). И для всех значений s=1, ½, -½, -1. И вот какие результаты получены для s=-½. Условно полученные интегралы мы назвали «зарядами».
(20) Из этих графиков видно, что и электрическое поле и электрический заряд – это один и тот же график. Это одни и те же формулы, это один и тот же феномен, это одно и тоже. Только основная масса заряда формируется в микроскопической области. Электрическое поле – это размазанный в пространстве заряд. Аналогичные картины получаются и для всех остальных значений s=1, ½, -½, -1. Правда сходимость и картинка для лока (1,1) несколько хуже. Что можно сказать по поводу этих графиков? 1. Формулы для момента вращения для лока (1,1) весьма сложны. И простое умножение этих формул на r -1/2 вносит слишком большую погрешность в результат. Поэтому он получился такой ломаный. 2. То что интегралы сходятся, говорит о существовании некоторых новых инвариантов (кроме массы, спина и электрического заряда). Как мы знаем из физики, такие инварианты реально существуют. Например магнитный момент, а также те свойства, которые сегодня описывают квантовыми числами. Типа «слабое взаимодействие», «сильное взаимодействие», «барионное число», «лептонное число», «магнитный момент», «внутренняя чётность», «изотопический спин», и т.п. Это тоже означает существование за этими числами реальных физических свойств. 3. Из графиков (18), (19), (20) видно, на каких расстояниях формируется собственно заряд, а дальше начинаются свойства близкие к закону Кулона, законам Максвелла и закону Гаусса. 4. В принципе эти графики весьма похожи на ранее исследованные нами графики спинов элементарных частиц. 5. То что мы привели графики для поправки на r -1/2 не означает, что именно она формирует электрический заряд. Дело это тонкое и легко ошибиться. Это дело молодых физиков будущего, владеющих Маткадом и Мапле. Мы затронули новый пласт теоретических исследований. Физика становится теоретической и математической. Что лучше: содержать 100 хорошо владеющих математикой физиков, или миллионы работников среднего уровня на строительстве и обслуживании коллайдеров? Может пусть они лучше жилые дома или дороги строят? Таким образом, окончательный вид формул зарядов элементарных частиц такой. q=k•r, величины k для всех частиц разные, зависят от массы. L1 и L2 – коэффициенты Ламе для гукуума. Электрон. Формула (с точностью до коэффициентов) для момента вращения (спина):
(21) Формула для заряда (далее нам пришлось поменять обозначение с L на Q, потому что L1 и L2 заняты под коэффициенты Ламе, все буквы заняты, не хватает букв) Q0,0(q):
(22) То есть та же самая формула, но подъинтегральное выражение умножено на r -1/2 . Аналогичные формулы для нейтрона. Спин:
(23) Заряд Q1,0(q):
(24) Аналогичные формулы для протона. Спин:
(25) Заряд Q1,1(q): (26) Графики этих интегралов (18)-(20). Но пока это только гипотеза насчёт коэффициента на r -1/2 в знаменателе. Нужно тщательно исследовать подъинтегральное выражение rs , где s – некоторый ряд чисел, имеющих физический смысл. s=1, ½, -½, -1. А возможно и какие-то другие варианты. Выводы. Мы изложили план теоретических исследований зарядов элементарных частиц. Получены некоторые предварительные результаты. Мне, Дубинянскому А.И. уже 66 лет, диабет, здоровье. Возможно, это моя последняя научная статья. Далее нужно финансирование и подключение группы хороших физиков и математиков. Из тех сотен миллиардов долларов, которые впустую затрачиваются на коллайдеры, можно и нужно ответвить струйку в несколько миллионов на детализацию теории Упругой Вселенной. Литература. 1. Яворский Б.М., Детлаф А.А. Справочник по физике. «Наука», 1980. 2. Ландау Л.Д., Лифшиц Е.М. Теория поля. «Наука», 1988.
Назад
Главная страница
Оглавление
Далее
Страница размещена на сайте в мае 2005
года |



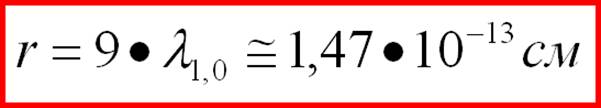

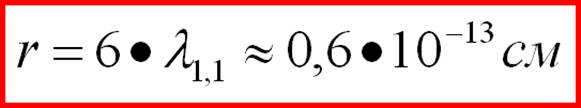
 (1)
(1)  (3)
(3)  (6)
(6) 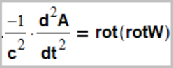 (7)
(7)  (8)
(8)

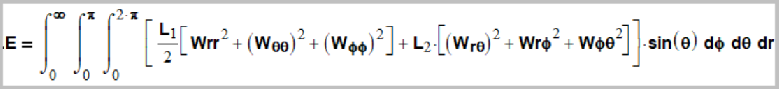
 (15)
(15) (16)
(16) (17)
(17) 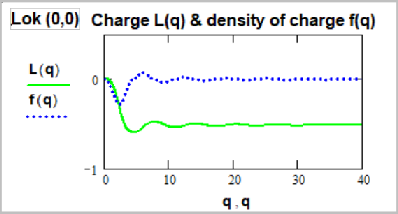 (18)
(18)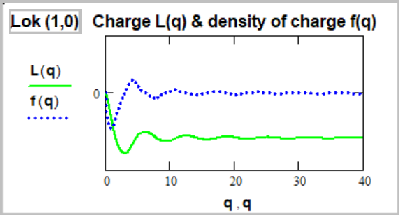 (19)
(19)