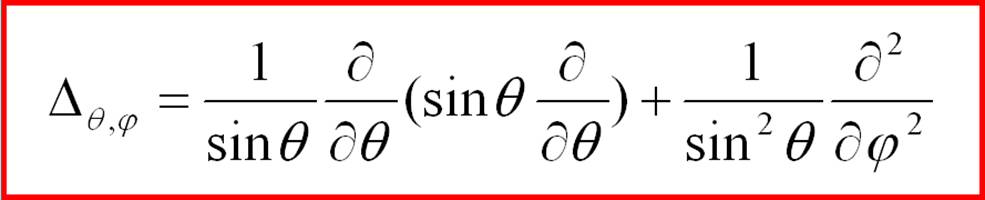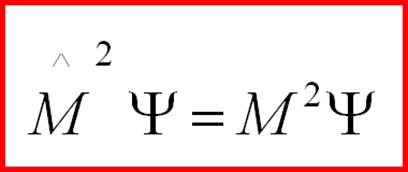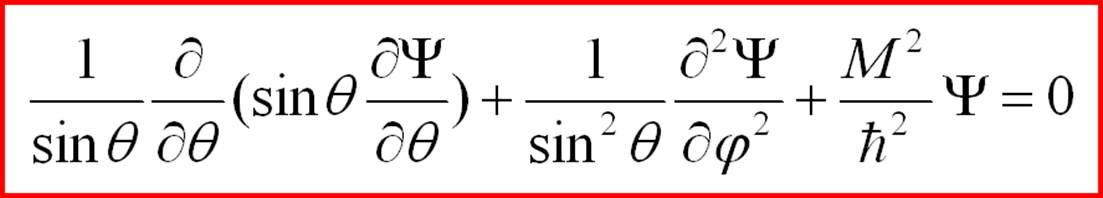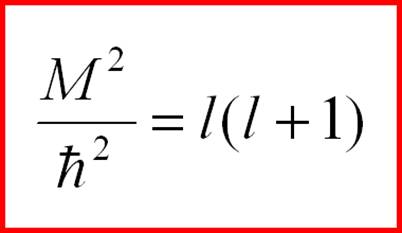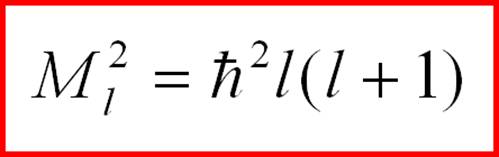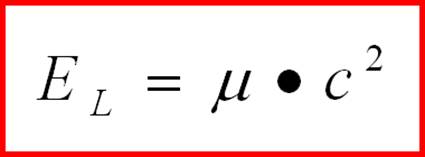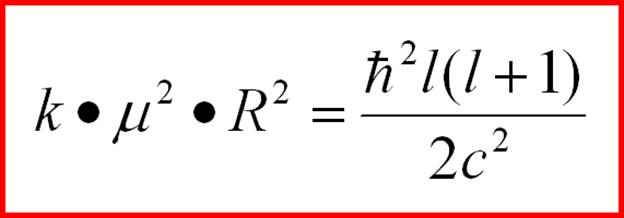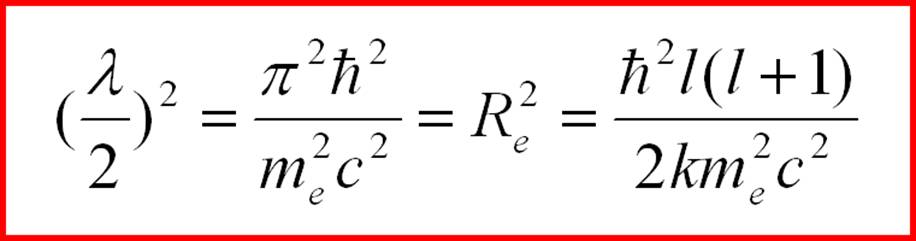Рассмотрим  квантование момента импульса "микрочастицы". В общепринятой трактовке это квантование достаточно абстрактно, носит характер формальных математических операций. Тем не менее, это - общепринятая теория, фигурирующая во всех учебниках и носящая статус точного отражения объективной реальности. Наглядный смысл такое квантование получит только в теории Гукуума.
   Под моментом импульса понимается векторное произведение радиус - вектора частицы на ее импульс:   M = [rp] . В квантовой механике точно так же умножаются операторы величин M и p :

  Нас более интересует оператор квадрата момента импульса.

(2-26)

(2-27)

есть оператор Лапласа для сферы. Аналогично и проекции оператора момента импульса получаются зависящими только от угловых координат (q, j). Уравнение для определения собственных значений и собственных функций оператора квадрата момента импульса:

 (2-28)

или подставляя (2-26) и (2-27) в (2-28), получаем уравнение:

(2-29)

(2-30)

где l - целое положительное число. При каждом таком значении l существует (2l + 1) решений, которые представляют собой сферические функции. Собственные значения оператора квадрата момента импульса будут:

(2-31)

   l  = 0, 1, 2, …

   То есть, из уравнения Шредингера (которое, как мы показали, эквивалентно волновому уравнению) с необходимостью следует дискретность квадрата момента импульса объекта, независимо от внешнего вида этого объекта. В частности, этими объектами могут быть и  локи.  Более того, если мы "в лоб" решим волновое уравнение, потребуем "непрерывности и однозначности" решения, то после разделения переменных неизбежно придем к уравнению (2-29). Только там будет стоять квадрат момента вращения лока  M² .   И совершенно справедливо будет сказано о нем то же самое, что значения квадрата момента импульса лока будут дискретны и определяться по формуле (2-31).
   При  l = 0  существует решение уравнения (2-29). Это константа. Чему равна эта константа, видно, например из формул для спинов элементарных частиц.
   Таким образом  всего лишь из требований конечности, непрерывности и однозначности решения (2-29), а следовательно и (2-1), возникает квантование, возникают дискретные уровни! И при этом никакие другие значения всех перечисленных выше величин не могут реализоваться в природе!
   Будем считать это  четвертым сигналом в пользу теории Гукуума.
   Развиваем эту мысль. Классическое решение волнового уравнения сразу предлагает нам дискретный спектр решений. Математика дается нам свыше и ее законы абсолютны. Следовательно, применяя математические законы к описанию Гукуума, можно сделать вывод, что Гукуум допускает и пропускает в себе не абы какие колебания и их изменения, а колебания и изменения дискретные. Возможно, что недискретные решения волнового уравнения также существуют в Гукууме. Но эти решения никак не влияют на мир, в котором мы живем. Нам не дано узнать, существуют ли они или наш мир единственный. Также пока открыт вопрос о существовании миров с другим уровнем дискретизации, с другой постоянной Планка, которые тоже могут проходить сквозь нас, а мы сквозь них без всякого влияния и взаимодействия.

   Теперь обратим внимание на энергию  лока.  Полученное выше доказательство дискретности квадрата момента импульса объекта в нашей теории Гукуума имеет объективный и однозначный характер. И за этой дискретностью с необходимостью тянутся другие дискретности. Если принять во внимание формулу из механики:

(2-32)

                      l = 1,2,…           

   Энергия неподвижных локов может меняться.  Эти вихри могут поглощать энергетические кванты. И вопреки существующему мнению , предполагается, что  свободные электроны могут поглощать фотоны.  Надо только проделать соответствующие эксперименты, а не ссылаться на устаревшие теоретические выкладки. Но энергия и масса связаны неразделимо, следовательно,  и масса локов имеет дискретный спектр.
   Далее, если представить момент инерции  лока  в виде

   где величины в правой части, соответственно: k - некоторый коэффициент (без особого физического смысла, будет уточнен ниже), масса  лока  и квадрат его эффективного размера, то учитывая (2-9) в виде

(2-35)

   и подставляя (2-34) и (2-35) в (2-33), получаем  новую  формулу  связи  между размером частицы, ее массой и степенью ее энергетического возбуждения:

   где по-прежнему  l  равно любому целому числу. Правда кроме нуля, но сейчас не будем заострять внимание на этом. Можно предположить, что в невозбужденном состоянии, то есть при  l = 1  должна получиться формула для  комптоновской длины волны  элементарной частицы (2-12). Сравнивая формулы (2-12) и (2-36), получаем, к примеру, для электрона:

   откуда

   Как видно, результат не зависит от того, какой лок рассматривается, электрон или протон. Как видно из (2-38) и (2-34), момент инерции элементарных частиц растет с ростом их энергетического возбуждения.
   В общем-то здесь возникает противоречие с общепринятым мнением, что элементарные частицы не имеют энергетических уровней в свободном состоянии. Но мы идем по непротоптанным маршрутам…
   Главное для нас сейчас - численная оценка коэффициента k. При невозбужденном состоянии  лока, то есть  l=1,  получается значение величины  k  равное приблизительно 0,1. Запомним эту величину для нижеследующего изложения.
   По-видимому, разница коэффициентов в формулах для спина электрона (S_e = √3/2 ћ) и спина протона (S_p = 1/2 ћ) появляется из-за разницы геометрической формы этих локов, то есть из-за разницы в параметре  l  в формуле (2-38). Но это число характеризует и энергию возбуждения. Кто-то из них всегда более возбужден.
   Рассмотрение формулы  (2-36)  обнаруживает, в принципе, способность "частиц" увеличивать размеры не меняя их массы. Или увеличивать массу при постоянном размере. Или и то и другое. Что происходит на самом деле вполне вообразимо в свете теории Гукуума, но надо работать, уточнять, детализировать.
   Что еще открывает уравнение  (2-36),  так это прямой путь к возможности очень больших элементарных частиц (пусть и недолго существующих). Проделанные выкладки, возможно, пригодятся нам ниже, при описании  шаровой молнии,  которая предположительно является одним из подтверждений формулы (2-36) для  l ≈ 10³⁰ .
   Более позднее замечание. Впоследствии оказалось, что для шаровой молнии существует вообще другое решение в классе локализованных решений.
 

--- ---