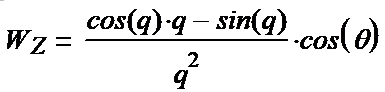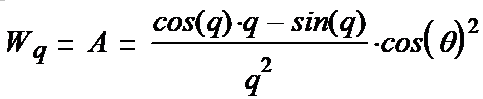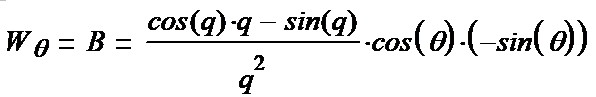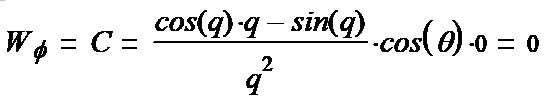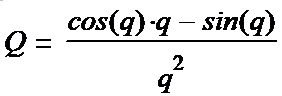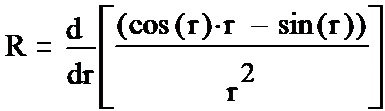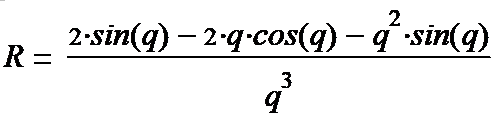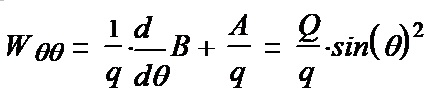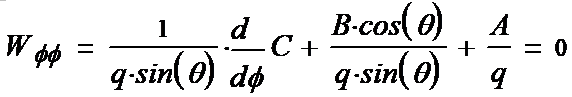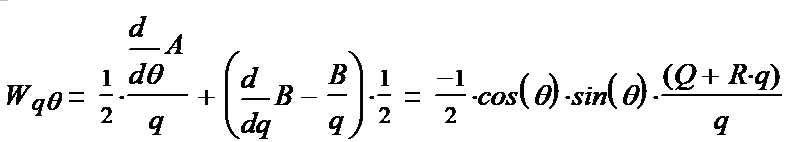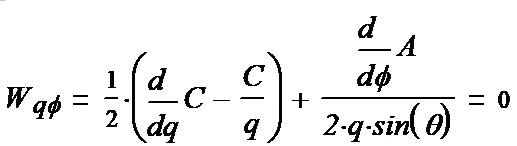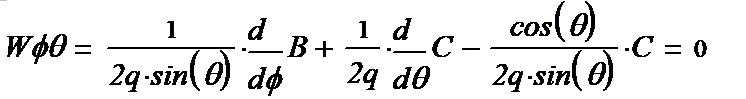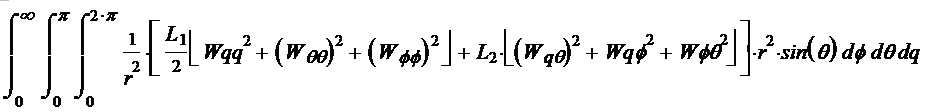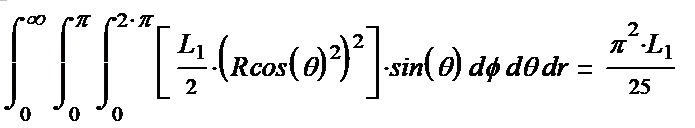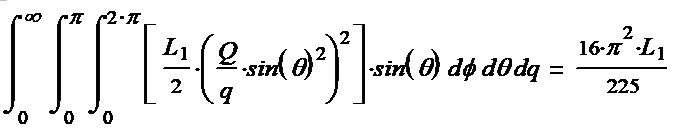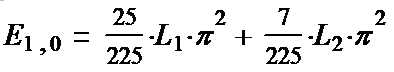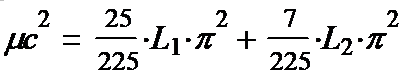Below this procedure is shown for the simple case j = 1 and m = 0. What kind of particle, we do not yet know.
   The displacement formula in a vertically placed lok. The dependence of W on the angular coordinates is absent. The dimensionless radial coordinate is used  q=k•r. k – coefficient, depending on the real mass of the particle.

(1-22*)

   The coefficient under the square root is temporarily omitted. Put it in the end. What is the coefficient k. This is nothing more than a link between ω in the vibrational part of the solution and the radial coordinate in the Bessel function: ω = k * c, c is the speed of light. The physics is such that in each particle (in each solution), due to physical reasons, the frequency of the wave traveling in a circle is set. Physical causes are determined by the form of the solution, and the way the solution is wound up on itself, and how the whole system stabilizes to a stable state. Also, particles have excited states. This issue has not yet been investigated. This can only be observed. Thus, all further solutions and formulas are only an illustration of the state in which all the wave vortices are located = loks = elementary particles.
   We have three displacement components as in (1-13):
 

(1-23*) (1-24*) (1-25*)

   We introduce useful notation:

 We write out the components of the tensor (1-15):

(1-26*) (1-27*)  (1-28*) (1-29*)  (1-30*) (1-31*)

Now try to write out the formula for energy:

(1-32*)

Here: in the center, in the square bracket is the expression for the energy density itself. On the right after the parenthesis is the expression for the volume element. Left before the bracket is the expression (1 / r²) for the law of winding.
   So, we get six triple integrals. Glory to computer programs that give us access to knowledge of elementary particles! This is a new horizon of science.
    We calculate these integrals. We calculate each separately.

 

   We get a solution:

 

(1-34*)

   This formula is something that relates the elastic properties of Gukuum  L₁ and  L₂  with the mass of (supposed!) elementary particles and the angular velocity of their rotation. Applying the formula of Lord Kelvin, we obtain:

 

(1-35*)

While we do not know what kind of particle it is. Two such equations for two different loks will make it possible to determine L₁ and L₂ of cosmic Gukuum.