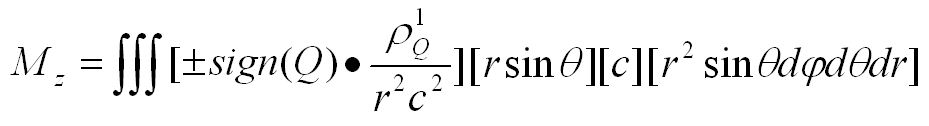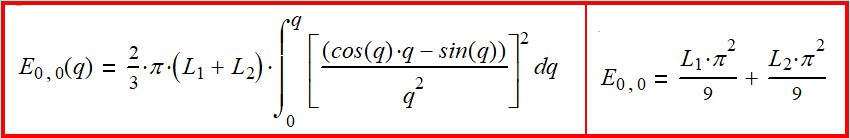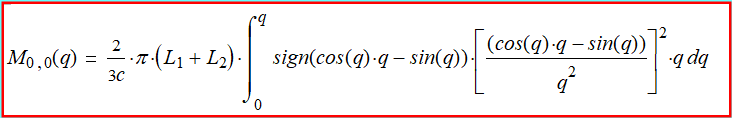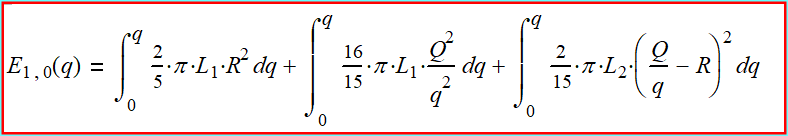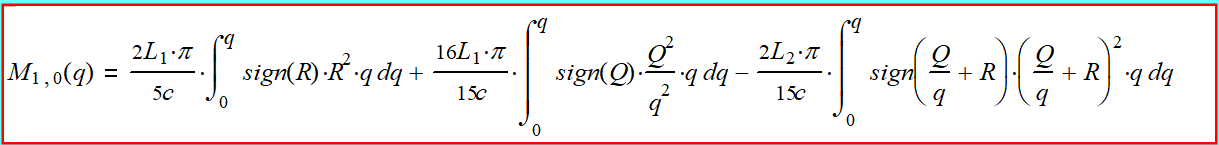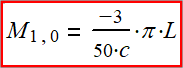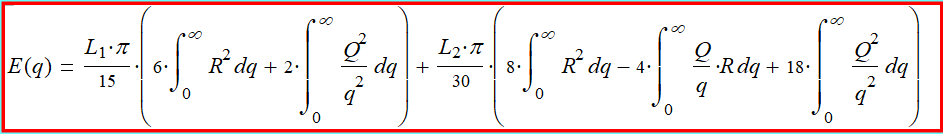Опубликовано: https://www.academia.edu/34522333/The_angular_momentum_of_the_lok

Уточнение: https://www.academia.edu/35952051/Angular_moments_spins_of_wave_vortices_loks_._Refinements

Обсуждение: https://www.academia.edu/35952030/Angular_moments_spins_of_wave_vortices_loks_._Refinements

http://vixra.org/abs/1802.0239

1. The essence of the hypothesis.
   Our mathematical model is that:
1. The universe is a rigid elastic continuum. This continuum
does not have any numeric parameters or constraints. This continuum may not have any mass or density. But by virtue of the law of conservation, it has some resistance to deformations.
2. In this continuum ALWAYS existed, and ALWAYS will exist all kinds of waves. The movement of the waves creates the whole picture of the universe that we observe. Including wave vortices create material particles. Mathematical descriptions are attached.
3. All visible and invisible objects of the universe, from large to small, are wave objects in this continuum. All visible and invisible objects of the universe, from large to small, are solutions of the wave equation:

(1-1)

4. All wave objects in a gukuum are described by an algebraic task
parameters of elasticity of a solid body and a three-dimensional wave equation. When
This simply assumes that these are "small" and "linear" waves. All questions like "what is" does not make sense. Continuum and everything.
5. As physical = letter parameters it is convenient to use the Lame coefficients L₁, L₂, L₃ (these are elementary combinations of the coefficients of compression, shear and torsion of a solid body). There are no numerical restrictions on the Lamé coefficients. Just the coefficients of Lame L₁, L₂, L₃ and everything.
6. Thus, the universe and all the matter contained in it are described only by letters, algebra. However, objects can be compared numerically. For example, the mass of the proton wave vortex can be numerically compared with the mass of the electron wave vortex.
7. All elementary particles, fields, photons, ball lightning, even lightning, dark matter are different types of solutions of the wave equation. So far we know several types of solutions to the wave equation, three spherical and three cylindrical, but perhaps this universe is not limited to.
8. The nonlinearity that exists in the universe is explained by the law of "winding a linear solution on itself". This is a very important law that makes it possible to understand the formation of elementary particles. As a result of such winding, or layering, the linear solution becomes non-linear and creates all the variety of the material world. This law consists in adding to the integral for the energy a factor  1/r².

 
2. Calculation of angular moments (spins) of loks.
   Next, everywhere we work in spherical coordinates.
   So, we take in mind the wave whirlwind = lok, and position it so that the wave rotation occurs around the Z axis. We assume that all the oscillations in the lok occur in the same direction. So it or not, we do not know yet. But this assumption is close to the truth. It is true in the first degree of approximation. This is our mathematical model. We locate the loks so that these oscillations in the lok occur along the Z axis, and the wave itself runs around the Z axis. Similarly, the lok energy moves around the Z axis. And in exactly the same way the movement of the energy of the lok creates an angular momentum = spin. 

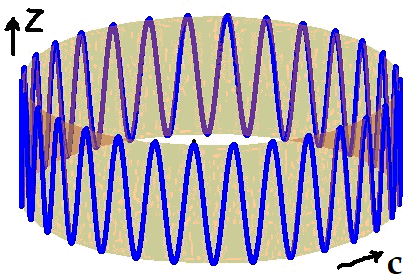
Fig.1.

Figure 1 shows a fragment of a wave traveling around the Z axis. The oscillations in it are directed along the Z axis. And the wave runs around the Z axis. As will be seen from the following, the carrier frequency (in blue) is constant on the entire wave vire. However, with the distance from the Z axis, the amplitude of the traveling wave changes. In addition, with the distance from the Z axis, the angular velocity of the wave changes. That is, the outer layers are lagging behind the inner layers.
    Next, we use the materials outlined in the previous article.
We go for simplicity to the dimensionless length: 

(2-1)

Useful formulas:

(2-2)

   Heuristic assumption.
   To calculate the angular momentum, it is necessary to integrate the angular moment of all infinitely small elements of the wave vortex. A heuristic assumption was made: the sign of the functions Q and R standing in quadratic forms for the energy of the loks precisely determines the direction of motion of this energy element. This is quite logical, and a fairly consistent assumption. Analysis of the formulas for the lok energies, analysis of the formulas for R and Q, the absence of an angular dependence on φ in them, shows that in this case the energy in the loks rotates as if by spherical layers around the Z axis. In determining the direction of motion of the layers of mass = energy of simple loks (0,0) and (1,0), only one variable q participates. When moving from layer to layer, the direction of energy movement can even be reversed. But if the sign can be fixed, then the sign itself or the direction of the movement of the element in at least one layer is not yet possible to determine. Therefore, all the formulas given below are valid "to the contrary".
   Thus, a plausible general formula for the angular momentum of the simplest loks M_z has the form: 

(2-3)

ρ¹ energy density of an element of volume.
ρ¹_Q - part of the energy density depending on Q.
Q - previously defined auxiliary quantity.
    Under the integral sign are four elements, which are highlighted in square brackets for clarity. The first square bracket contains the elements of the mass density of the lok (the difference from the energy - c² in the denominator), taking into account the "stratification" ( r² in the denominator) and also taking into account the sign with which this mass will enter into the angular momentum formula (function sign). That is, depending on the direction of rotation of this element. The second square bracket is the distance from the axis of rotation to the Z axis. The third square bracket is the velocity of the mass element, the speed of light. The fourth is an element of volume. That is, it is the moment of the impulse in the classical sense of it.
    The integrand can contain several functional dependencies, depending on the complexity of the lok (m,n).

Lok (0,0).

(2-4)

The general equation for the angular momentum, according to formula (2-3): 

(2-5)

The distribution of the angular momentum and the distribution of the angular momentum density inside the particle as a function of the radius are illustrated by the behavior of the integral and the integrand in (2-5):

Fig. 2.

As seen from the graph, the spin density at infinity tends to zero, and the moment itself asymptotically approaches a certain value, approximately equal to: 

(2-6)

Lok (1,0).

(2-7)

As can be seen from formula (2-7), in the lok (1,0) there are, as it were, three functional "nuclei" of spin formation. it  Q , R. In addition, the sign function contains the angular coordinate θ. The general equation for the angular momentum, according to formula (2-3): 

(2-8)

Assuming that  L₁=L₂=L, which in most cases is valid for all terrestrial materials, we obtain the following graphical dependences of the radial distribution of the angular momentum and the density of distribution of the angular momentum inside the particle as a function of the radius. Without correction factors:

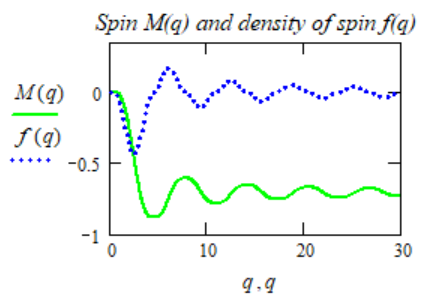
Fig. 3.

As seen from the graph, the spin density at infinity tends to zero, and the moment itself asymptotically approaches a certain value equal to approximately: 

(2-9) 

Lok (1,1).

(2-10)

As can be seen from formula (2-10), there are also three "nuclei" of spin formation in the lok (1,1). But they are reduced to the same three: this  Q , R  and  Q•R.  In addition, the function  sign  contains angular coordinates  θ  and  φ. The triple integral with sign functions inside is very complicated, so there is no complete certainty that we did everything right. The general equation for the angular momentum, after integration with respect to the angular coordinates, according to formula (2-3):
 

(2-11)

It should be noted that the coefficients in the formula for the energy and in the formula for the moment are significantly different. This is due to the fact that dependencies on angular coordinates appear in the lok (1,1). Which, after a rather complex integration (because of the presence of the sign function) lead to such coefficients.
Assuming that  L₁=L₂=L , which in most cases is valid for all terrestrial materials, we obtain the following graphical dependences of the radial distribution of the angular momentum and the density of distribution of the angular momentum inside the particle as a function of the radius. The correction factor, so that both graphs are visible, for M is equal to 0,2.

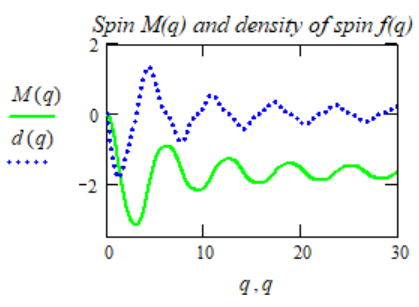
Fig. 4.

As can be seen from the graph, the spin density at infinity tends to zero, and the moment itself asymptotically approaches 0.3. Taking into account all the coefficients adopted on the scale graphs, the moment of the lok (1,1) is approximately: 

(2-13)

Comparing the angular moments (spins) of loks does not make much sense. Because solutions have constant coefficients, different for all solutions. But the participation of young and strong mathematicians and physicists will make it possible to clarify the problem of identification between real particles and loks. 

Other loks.
    As our check shows, loks (3,1), (3,2) and (3,3) also have finite, computed angular moments. Therefore, the identification of elementary particles is still difficult. Also, we can not say that having the spins of loks by formulas (2-6), (2-9), (2-13), we can compare them with each other. These formulas are obtained on the assumption that  q=k•r , and the coefficients k are related to the real masses of the particles. These masses are different. In addition, in each solution a constant at the beginning is possible, which is traditionally determined only on the basis of real masses and spins. Other considerations we have not yet. Therefore, we are still postponing the identification of elementary particles. We assumed that lok (1,0) is a neutron, and Lok (1,1) is a proton. Based on the similarity of the charge distribution graphs inside the neutron and the spin inside the lok (1,0). However, our friend Warren R Giordano said that the neutron is more complex, so it is not stable. That is, most likely the neutron is a lok (1,1). Now, Loks (3,1), (3,2) and (3,3) are connected to the review. We'll keep thinking.

Назад    Главная страница     Оглавление     Далее  

--- ---