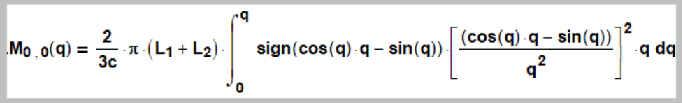|
Назад Главная страница Оглавление Далее Опубликовано: https://www.academia.edu/34532615/Electric_charge_and_spin_of_elementary_particles http://vixra.org/abs/1904.0243 Electric charge and spin of elementary particles. AT THE BOTTOM ANNEX ON 12.04.2019. Abstract. The graphs of the distribution of the electric charge and spin inside the elementary particles are compared. The proximity of the physical essence of the values of the electric charge and the spin of elementary particles is established. Below we use information and
graphs about the "structure of nucleons" from the same
reference book Javorsky - Detlaf [10]. Regarding
the charge and other quantities. Electron and other
particles are localized wave objects. These objects are
characterized by a volumetric distribution of the amplitude
of oscillations of the carrier-gukuum and their shape. On
the basis of the volume distribution of the wave amplitude,
several derived quantities can be made up from it. -------------------- In traditional physics, the concept of electric charge is introduced to illustrate the interaction between particles. Readers are so used to this concept, to the convenience of working with this concept, that they perceive it as an objective reality. That is, everyone believes that the electric field, like the magnetic field, as well as the gravitational, as well as matter itself, elementary particles - all this really exists. How else? All this is perceived either by our senses or by instruments designed for our senses. Even a boson is invented, similar to the Higgs boson, which is the charge carrier.In the theory of the Elastic Universe, there is only an infinite elastic space - the gukuum and there are all kinds of its stress fields in this gukuum. That is, there is a stress field tensor of 3x3. The squares of the values of the components of this stress tensor determine the 9 components of the energy density of the stress field at a given point. The sum of the squares of these 9 components of the stress tensor determines the total energy density at a given point. These are the foundations of the theory of elasticity, they are set forth in any textbook. It is known that the tensor 3x3 is reduced to diagonal form. There are only three diagonal terms. This is the reason that there are only three "fields": electric, magnetic and gravitational. Although these fields are not described only by the diagonal terms of the stress tensor. Thus, if this stress tensor in gukuum is brought to diagonal form, then the remaining 3 diagonal components of the stress tensor determine three types of "fields" in our physical sense. Of course, this applies only to a fixed point in the space of the gukuum. Invented by physicists of the so-called. strong or "weak" interaction in reality have another explanation, which does not go beyond the stress tensor in gukuum. The fields considered in physics, electric and magnetic (and gravitational) are determined by their strengths. These values are taken very subjectively. Thus, the electric field is introduced in the experiment on the interaction of charged bodies, and the magnetic field in the interaction of electric currents. Therefore, their relationship to the components of the stress tensor in gukuum is determined through some combinations of the proper component of the stress tensor and their derivatives. And these combinations are very different. For the same reason, the search for a "magnetic monopoly" is unsuccessful and meaningless. In the same way as an electric field, the concept of an electric charge of a particle (electron, proton) is subjectively introduced. That is, a charge is in some way a definable quantity that estimates the property of particles to be attracted to each other or repelled from each other. Since physicists have not known the mechanism of interaction of "charged" bodies up to now, the charge model suited everybody. Type of what can be a property of "charge" to endow blondes and thereby explain their attractive ability. In the theory of the Elastic Universe, the ability of particles to attract - the repulsion arises and comes from the ability of their localized waves (from which all particles and all matter consist) to slightly influence each other at their spatial intersection. Depending on the direction in the intersecting waves, there is either attraction or repulsion. Since each particle in the theory of the Elastic Universe consists of the wave spheres rotating around the axis (an infinite number, but their amplitude rapidly falls already on 4 spheres), which alternately rotate either in one direction or in the opposite direction (this is not a fantasy, it is a strict mathematics), then the total interaction between the particles is determined by the total interaction of all the wave rings of a given particle.
This is a drawing of a neutron. With the exact formula. The
neutron consists of concentric wave spheres rotating around
the vertical (in this figure)
Z
axis.
In the figure: the portrait of an electron (approximate) and
the formula for it (absolutely accurate). Moreover, none of
the wave rings that make up the body of an electron can be
removed or separated. There is no such power in nature! And
the funniest thing: all these rings rotate around the ring
at the speed of light, but the neighboring rings rotate in
opposite directions. The amplitude of these circular waves
at the point of contact of the rings drops to zero. And
this, too, is not a fantasy, it is a strict mathematics.
Plus confirmed by the comparisons given below with the
experiment.
It
turns out that scientists have been interested in these
issues for a long time. Experiments were conducted in the
1960s and 1970s, when nobody knew about the model of the
Elastic Universe and did not suspect anything. The internal
arrangement of elementary particles was an absolute mystery
to all. I remember, and in my student years (1971-1977,
MIPT) I often thought: how are they arranged inside? What is
this solid electronic that rotates around a solid proton?
Why does it rotate so steadily, despite all collisions with
surrounding electrons ?! Why does not it fall on the nucleus
of an atom? Where do quantum laws come from? Comparison
of the available experimental data with the available
theoretical results.
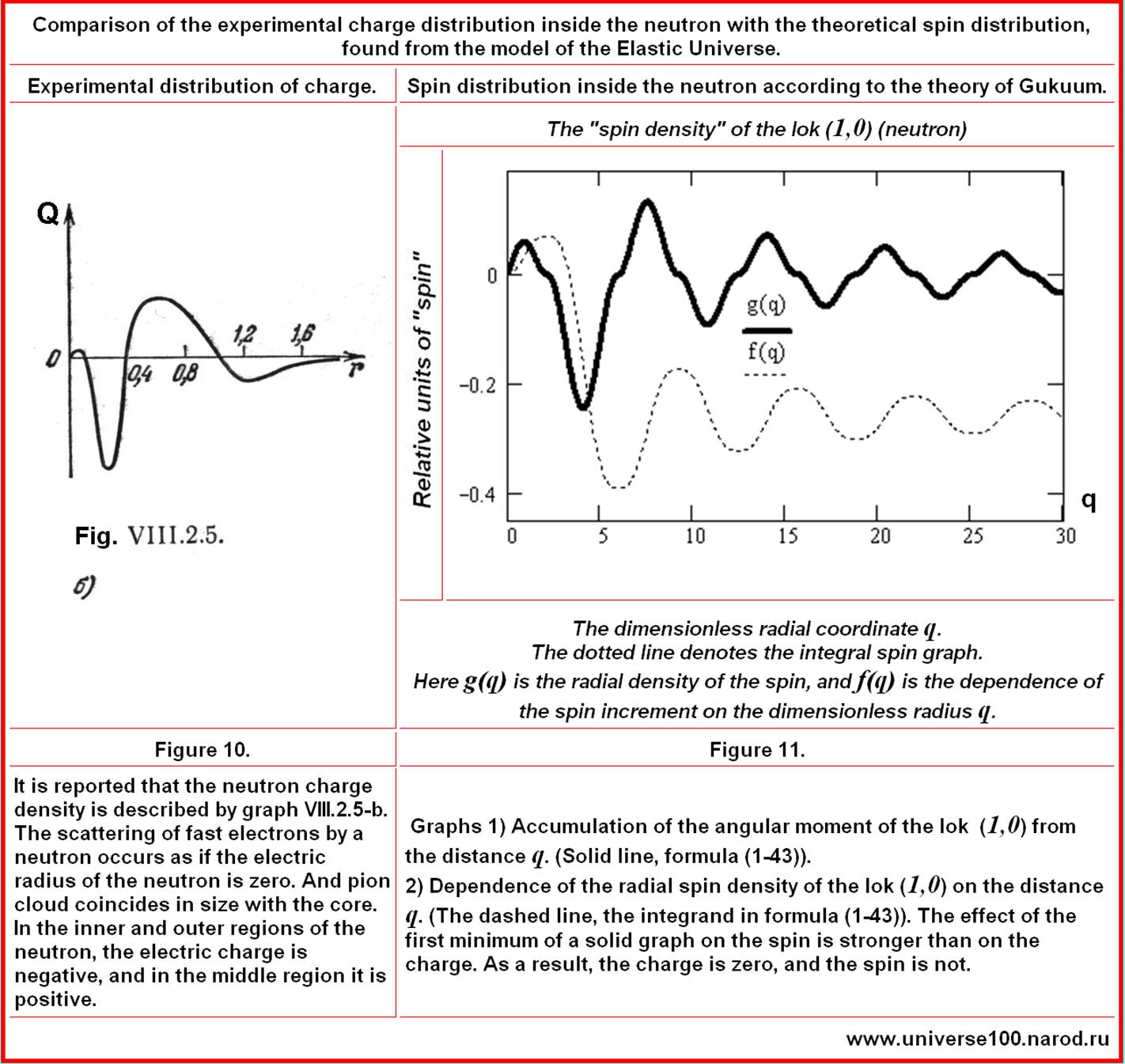
The comparison is shown in the table below. We slightly
changed the first picture in comparison with the book,
because there was an overlay: on it the letter
q
denotes the density of electric charge. And we, unknowingly,
in our theory designated
q
as a dimensionless radial coordinate. Well, it's clear,
someone will get confused, make a noise, and blame us all.
Therefore, we designated the charge density as
Q.
Comments. Here, in the figure to the right, a solid solid
line designates the radial distribution density of the spin
inside the assumed neutron. A dotted line is the integral
density of the spin as a function of distance.
(1-58)
Exceed the theory over the experiment, 2 times. But the
experimental data were treated as bombardment of a neutron
by a point electron. But in reality the electron is huge ...
Maybe the dimensions of the electron are superimposed on the
results of all the experiments. Or what other reason.
The order of
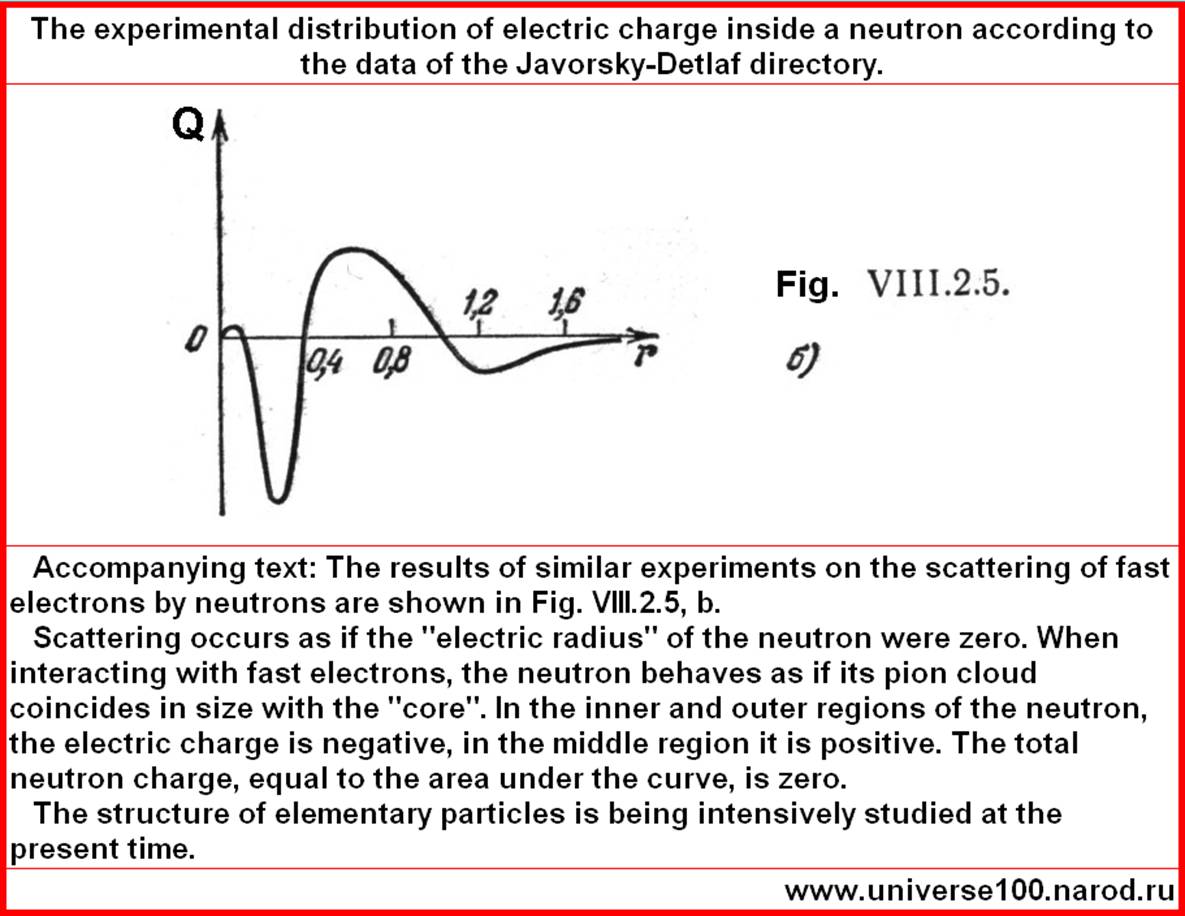
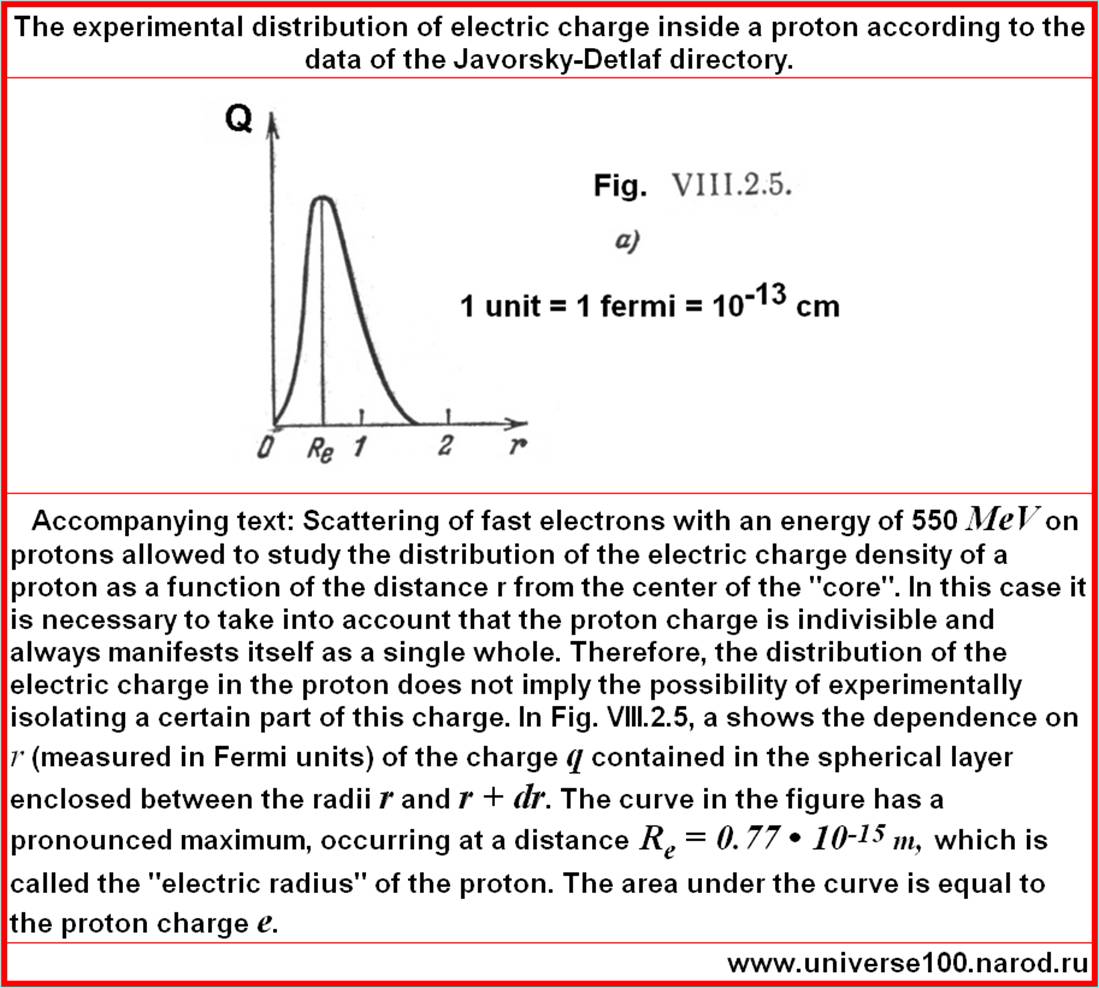
magnitudes is important. The following graph shows the distribution of the charge inside the proton, according to the same studies of the 1960s and 1970s. The peak of the charge density inside the proton is visible. The rest of the charge distribution curve, both inside the proton and inside the neutron, scientists could not display the 60-70s. Why? - Because the accuracy of measurements, trajectories decreases with increasing distance. The error grows, readings are smeared. Yes, and the model that explains all this was not.
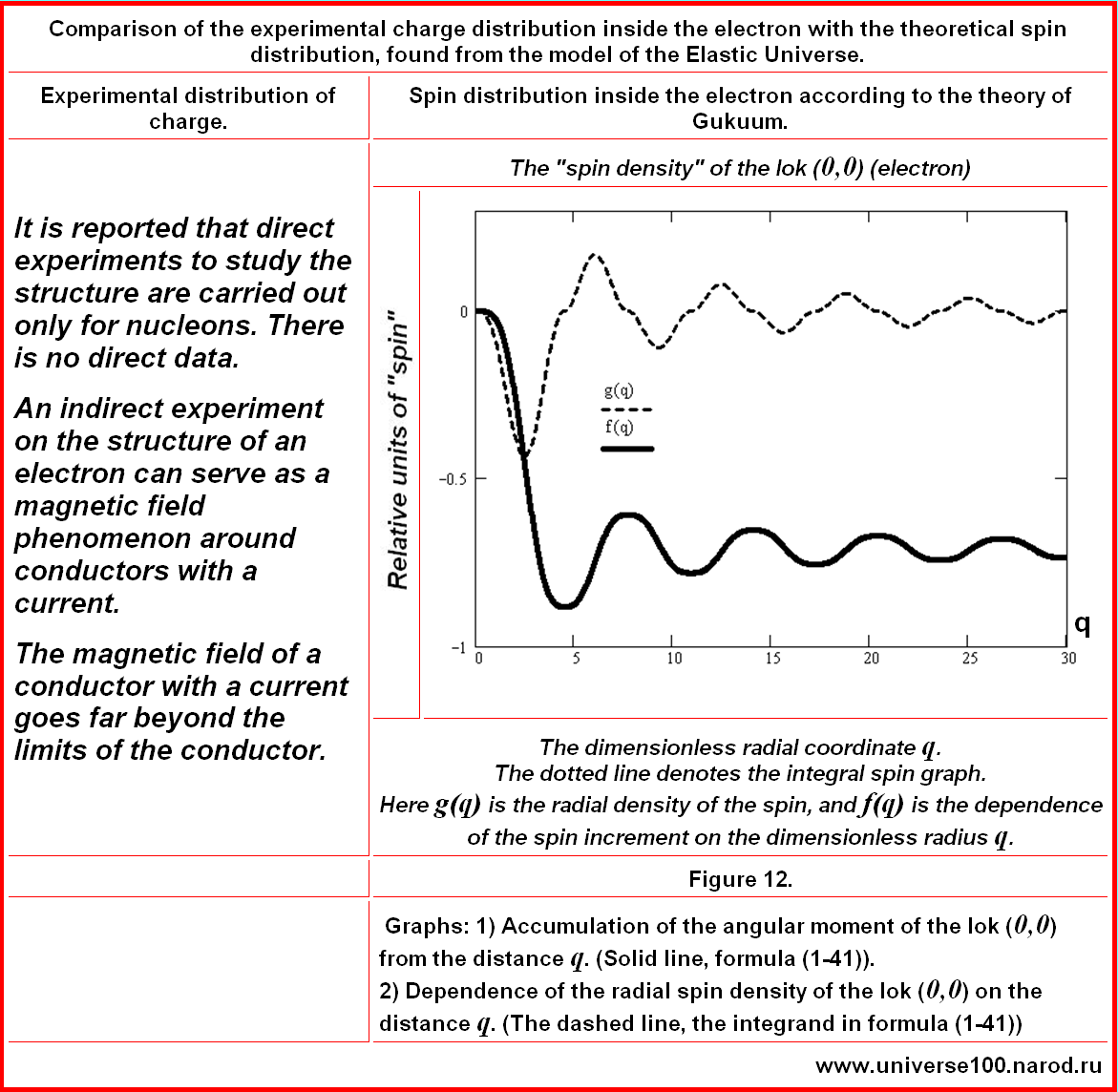
Below on the right graph is our theoretical spin distribution within the assumed proton according to the theory of the Elastic Universe. Recall that according to our explanation given at the beginning of this report, the distributions of the spin and charge inside the particles must correlate, because to calculate these quantities, it is necessary to sum the alternating series, they must take into account the multidirectional motion of the spherical energy layers inside the particles.
Comments. Here, a solid solid line designates the radial
distribution density of the spin within the assumed proton.
A dotted line is the integral density of the spin as a
function of distance. It is very likely that the researchers were interested in what happens near the core of the proton. And they simply did not pay attention to fluctuations in the distribution far from the core. Perhaps they took this for random errors. Perhaps they did not contribute to the results and the publication because they did not know how to interpret these results at all. The maximum in the graph on the right is reached at q≈6. How much will it be in centimeters? In accordance with the (approximate) formula (1-55) we have:
(1-57) It is sufficiently close to the experiment (0.77•10-13 cm). However, all the near-proximity experiments and theories are not surprising after their energy density configurations coincided. --------------------------- Conclusions. In order to give exact theoretical formulas for the charges of elementary particles in the future it will be necessary to conduct painstaking and complex mathematical studies of the spatial distribution function of the vector stress fields in loks. However, there is evidence, with numerous other, not mentioned here, experimental confirmations of the theory of the Elastic Universe. And what do we have with the electron?
Comments. Once again,
we note that the signs of the spins of the alleged
elementary particles have not yet been specified. Also, the
ratio of signs in spins and charges is still unknown. We
also note the absence at the beginning of the graph of the
"bumpock" as in a neutron. This is more evidence of the
reality of the graph for a neutron. --------------------------- For future approximate estimates and experiments in which the spin and charge of an elementary particle appear, it can be assumed that
Q = k•S , (А)
where
Q is the
charge,
k is some
coefficient (which is very likely to be the same for all
particles), and
S is the spin
of the particle. Thus, for the proton and the electron this
assertion is carried out with obviousness. But for the
neutron, according to our theoretical calculations, there
remains the assumption that the neutron has a small back and
a small charge. Q = k•S + F(r,θ,φ) + …, (B) - - <> - - SUPPLEMENTATION FROM 04/12/2019.
Electric charge and electric field of elementary particles.
Abstract. The inaccuracy of the modern view of the electric charge and the electric field is shown. The whole theory of Maxwell, Coulomb and other giants of physics, is valid only for macroscopes, on the order of more than 100 sizes of elementary particles. In the microscale there are completely different laws. Including the field of a single charge does not have spherical symmetry and the Coulomb dependence is inverse to the radius.
Alexandr I. Dubinyansky and Pavel Churlyaev.
1. Introduction. The more mankind goes deeper into the knowledge of Nature, the more difficult it is to move. The concepts and mathematical formulas become more difficult. The lower the confidence of scientists to the published results. The theory of the Elastic Universe gave an answer to the origin of the mass of particles, the angular momentum of the particles. But in the matter of electric charge there was a delay. Mainly due to the distrust of scientists to our theory. What to take for the main axioms? Scientists proceed from generally accepted postulates. If we start from traditional physics, then Gauss's law is valid:
That is, the charge is equal to the integral of the divergence of the electric field. According to Maxwell’s equations:
And since there are no charges inside the wave vortices (locks), we will always get zero. What checked our analytical calculations. This is a mandatory procedure. Trust but check. We started from the equation:
Where A - electromagnetic vector potential obtained from our unified theory of all fields. All this we have long found, published in our previous articles. Further W – смещение в гукууме. As is known from mathematics, for any vector field W there is such a Helmholtz decomposition:
what:
According to our earlier conclusions, A – this is the electromagnetic vector potential, and G gravitational field strength. According to the textbook Landau - Lifshits
But given (5), you can write:
Thus, we can express the charge of any wave vortex through displacements W which we previously calculated and published 15 years ago. The charge is expressed as an integral over space-time.
We have done all calculations for lok (0,0), (1,0) and (1,1). And as expected, they got zero everywhere.
q=0 (9)
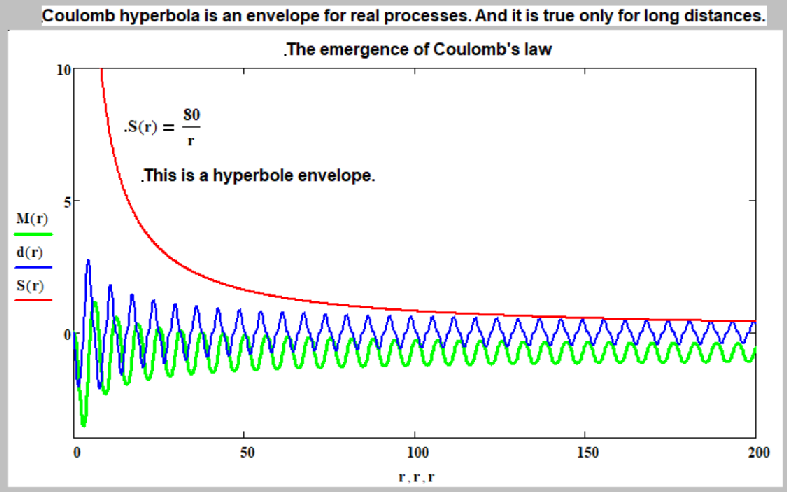
There was a similar story with the moment of particle rotation. The moment of rotation of the locks during formal integration also gave zero. However, after we took into account the direction of rotation of the elements of lok, the result was non-zero and meaningful integrals. What does this result mean? It means that physicists currently do not know what a charge is and what an electric field is. The basis for the description of the electric field and charge is taken simple, beautiful, idealized mathematical model. Model of Maxwell, Coulomb, and Gauss equations. In which, as it were (formula 2), the charge is separate, and the electric field is separate. The story, which was fixed and continued with the Higgs boson, when all the elementary particles are separate, and their masses are separately, like weights in a pocket, in the form of the Higgs boson. We have long had a question. Physicists, nuclear scientists spend billions on the study of the destruction of protons. On relativistic research. But for some reason, interactions between charged particles at small distances are not investigated. Why? Yes, they are probably being researched, but they are not noisy about this, because all the laws in the microworld are violated and “wave functions”, “probability” and “uncertainty principle”, which violate the whole order, begin to work. What does it look like in reality? Coulomb dependence arises as an envelope of real processes in a wave vortex. At large distances (about 100 units on the graph) there is a complete coincidence with reality. But neither the Coulomb's law, the Maxwell laws, nor the Gauss formula work at small distances.
(10) This made us take a new approach to the calculation and description of the electric charge and electric field.
2. Charge dimension. If we compare the dimension of the spin and the dimension of the charge, we get. [Spin]: g1•sm2•sec-1 . (11) [Charge]: g1/2•sm3/2•sec-1 . (12) That is, we see the difference in the mass component and in the linear component. This fact we take further for the basis of the search for charge formulas of elementary particles. If our integral for calculating the spin included the energy density and the radial coordinate in the whole form, then it is very likely that these quantities should be included in the charge in a modified form. In particular, it is highly likely that the degree of the radial coordinate under the integral should be ½ less. This is certainly not the final conclusion. After all, the radial coordinate is included in the energy formula. What is the reason for the difference between the dimensions of spin and charge? As we have previously stated, based on physical properties, there is much in common between spin and charge. According to the directory Jaworski-Detlaf, close experimental graphs of their distribution inside the particles. The signs of these quantities are close. And the spin and charge of the neutron is zero. At the same time, we explained why an electron so small in mass has such a large spin and charge. This is a consequence of the large size of the electron, its large wave cloud. At the center of the electron, the density is zero, like a donut. The proton is very small and very dense, has a seal in the center of the "core". That is, comparing spins and charges, we conclude, for example for an electron, that the same elements of a wave vortex (0,0) enter into the formation of a spin and a charge. They come with the same signs, but for the charge these elements are multiplied by some functional coefficient. We will not guess about the exact form of this coefficient, because we do not imagine what is happening there at the micro level. This is a very difficult task for future young people. We will be satisfied with some approximation. The spins of the particles do not interact at a distance, and the charges interact. This is the important difference between spins and charges. But is it? Why are we so sure that when the two protons approach each other, the charges interact? This does not follow from anywhere. We might as well say that the spins interact. We do not know the processes at the micro level. It is possible that the interaction of the electron and the proton begins with the fact that the proton clings the electron with some of its elements, causes it to turn, and unfolds itself. And only then begins the interaction. Science does not know and does not understand this. This is referred to as “wave functions”, “probability” and “uncertainty principle”. Some components interact in the strain tensors of wave vortices. That is, in the tensors of Gukuum shifts. Well, the tensors of two electrons are the same, and their interaction is quite natural and understandable. But the interaction of the electron and proton tensors requires the search for some related components of the tensors. The existence of such related components is confirmed by the coincidence (up to sign) of the spins of the proton and the electron. Perhaps the direction of the search for such components. Let's try to compare the formula for the energy of the proton and electron.
(13) As you can see, there are identical elements, this Q . In this case, the parameter k in the formula q=k*r in formulas for (0,0) and (1,1) it is different, it differs by three orders of magnitude (approximately like the mass of a proton differs from the mass of an electron). Therefore, no synchronization of oscillations in the wave (0,0) and (1,1) can be expected. However, since the integral over r is taken to infinity, it may turn out that the presence of the parameter k does not matter. Таким образом весьма вероятно предположение, что во взаимодействии зарядов как раз играет параметр Q . In addition, this conclusion is valid. Since the experimentally established equality (in absolute value) of the spins and charges of the proton and the electron, we take this fact as a basis. That is, the same should be done according to the formulas. This is exactly what happens for the spins of a proton and an electron, but with a certain error. What formula and what the final result of the calculation of the spin is considered more accurate, for an electron or for a proton? Formulas for the proton are very complex, ambiguous, and cause little confidence. Therefore, it is better to rely on electron data. Let's try to act the method of selection.
3. Charge interaction. According to our theory of the Elastic Universe, elementary particles are single objects. There is no separation in them: this is a particle, and this is its gravitational field. By analogy with the planet Earth, here is the Earth, but its atmosphere. Or: this is the charge of a particle, and this is its electric field. In our understanding, this is a purely conditional division. In the same way, scientists once believed that "all bodies fall down." But then they found out that the “bottom” is also a body, the Earth. And they came to a more general formulation that “there is a gravitational attraction between all bodies”. Therefore, we choose a new path. Namely, based on the general formulas obtained by us for wave vortices, we will try to choose the formula of electrical interaction. So, 15 years ago we received an integral, which we called the "energy integral" of wave vortices (locks). At the same time, we used the “winding law”. We have made this integral, proceeding from traditional representations of physics, as the sum of squares of the elements of the strain tensor.
(14) We did all the necessary mathematical operations, and found that the energy integrals for the lok (0,0), (1,0) and (1,1) are safely calculated. Next, we made integrals similar to the rotational moment from traditional physics.
Here ρM – the density of the torque in the wave vortex, calculated according to standard rules, multiply the mass by the radius of rotation. Mass is energy divided by с2. Energy is calculated by the formula (14). We have done all these painstaking calculations with the help of Matkad, all the integrals have converged and have quite reasonable values. Matkad is very convenient, because the formulas from it are visual. Look at the formula (15). And if we showed here a formula from Maple, then no one would understand anything. Thus, based on the internal structure of the wave vortices, we obtained the masses and spins of elementary particles. All this was done 15 years ago and is in excellent agreement with the experiment. We obtained some integral formulas for wave vortices (14) and (15), which, as it turned out, have real manifestations. Integral (14) appears in the mass of particles. And integral (15) manifests itself in the moment of rotation (back) of the particles. We ask the question: are there any other integral values of the wave vortices besides the mass and the moment of rotation? Which could actually manifest themselves as some physical properties, except mass and back? For example, these integrals could be identified as an electric field, an electric charge, and even some new properties of elementary particles. As can be seen from the definitions and formulas, the torque is essentially the energy multiplied by the radius of rotation. Nothing mysterious. However, in practice such a simple multiplication adds one more physical property to the particle mass: spin. Why not try other combinations? We have previously established that in many respects the electrical properties of particles correlate with their spins. From these considerations, we make the assumption that the desired electric charge integral is closely related to the integral for the spin. That is, if the integral for the torque is calculated by the formula
That integral for electric charge can be calculated by the formula:
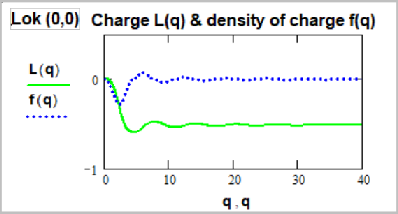
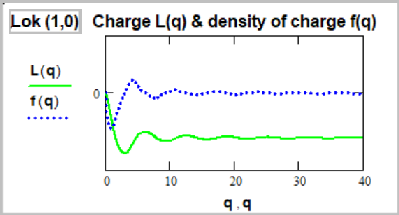
That is, with the addition of the subintegral expression rs , where s – some number of numbers that have physical meaning. s=1, ½, -½, -1. We took such a series of numbers because earlier in the study of the dimensions of spin and charge, we found just the difference on r1/2 . And values outside this area will give divergent integrals. We calculated integrals (17) for all three locks (0,0), (1,0) and (1,1). And for all values of s = 1, ½, -½, -1. And here are the results obtained for s = -½. The conditionally obtained integrals we called “charges”.
(20) From these graphs it can be seen that both the electric field and the electric charge are the same graph. They are the same formulas, they are the same phenomenon, they are the same. Only the bulk of the charge is formed in the microscopic region. The electric field is a charge spread in space. Similar pictures are obtained for all other values s=1, ½, -½, -1. True, the convergence and the picture for lok (1,1) are somewhat worse. What can be said about these graphs? 1. Formulas for torque for lok (1,1) are very complex. And simply multiplying these formulas by r -1/2 makes too much error in the result. Therefore, it turned out so broken. 2. The fact that the integrals converge speaks of the existence of some new invariants (except for mass, spin, and electric charge). As we know from physics, such invariants really exist. For example, the magnetic moment, as well as those properties that are now described by quantum numbers. Such as “weak interaction”, “strong interaction”, “baryon number”, “lepton number”, “magnetic moment”, “internal parity”, “isotopic spin”, etc. This also means the existence of real physical properties behind these numbers. 3. From the graphs (18), (19), (20) one can see at what distances the actual charge is formed, and then properties close to Coulomb's law, Maxwell's laws and Gauss's law begin. 4. In principle, these graphs are very similar to the previously studied graphs of spins of elementary particles. 5. The fact that we brought graphics for the amendment to r -1/2 does not mean that it forms an electric charge. The case is subtle and easy to make a mistake. This is the work of young physicists of the future, who own Matkad and Maple. We touched upon a new layer of theoretical research. Physics becomes theoretical and mathematical. Which is better: to contain 100 physicists well mastered in mathematics, or millions of middle-level workers in the construction and maintenance of colliders? Maybe they can better houses or build roads? Thus, the final form of the charge formulas of elementary particles is as follows. q=k•r, magnitudes k for all particles different, depend on mass. L1 and L2 – Lame coefficients for Gukuum. Electron. Formula (up to coefficients) for torque (spin):
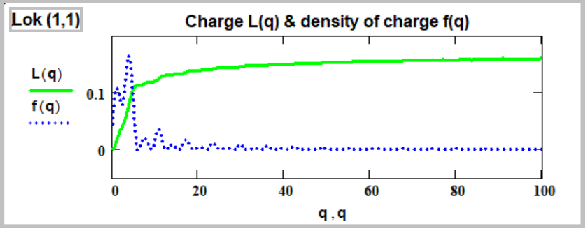
(21) The formula for the charge (then we had to change the designation from L to Q, because L1 и L2 busy under the coefficients of Lame, all the letters are busy, not enough letters) Q0,0(q):
(22) That is, the same formula, but the integral expression is multiplied by r -1/2 . Similar formulas for the neutron. Spin:
(23) Charge Q1,0(q):
(24)
Similar formulas for proton. Spin:
(25) Charge Q1,1(q):
(26) The graphs of these integrals (18) - (20). But for now this is only a hypothesis about the coefficient on r -1/2 in the denominator. Need to carefully examine the integral expression rs , где s – some series of numbers that have a physical meaning. s=1, ½, -½, -1. And maybe some other options.
Findings. We outlined a plan for theoretical studies of the charges of elementary particles. Some preliminary results have been obtained. I, A. Dubinyansky already 66 years old, diabetes, health. Perhaps this is my last scientific article. Next you need funding and connecting a group of good physicists and mathematicians. Of those hundreds of billions of dollars that are wasted on colliders, it is possible and necessary to branch off a trickle of several million to the specification of the theory of the Elastic Universe.
Literature. 1. Yavorsky B.M., Detlaf A.A. Handbook of physics. "Science", 1980. 2. Landau, LD, Lifshits, E.M. Field theory. "Science", 1988.
Назад
Главная страница
Оглавление
Далее
Страница размещена на сайте в мае 2005
года |



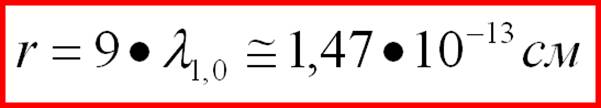

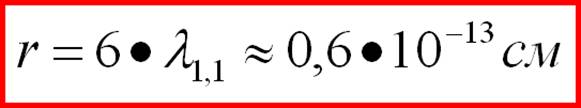
 (1)
(1) (3)
(3) (6)
(6)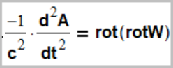 (7)
(7) (8)
(8)

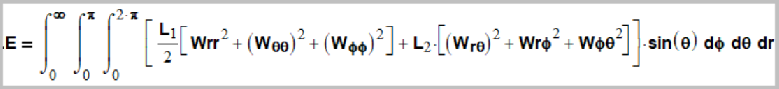
 (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19)