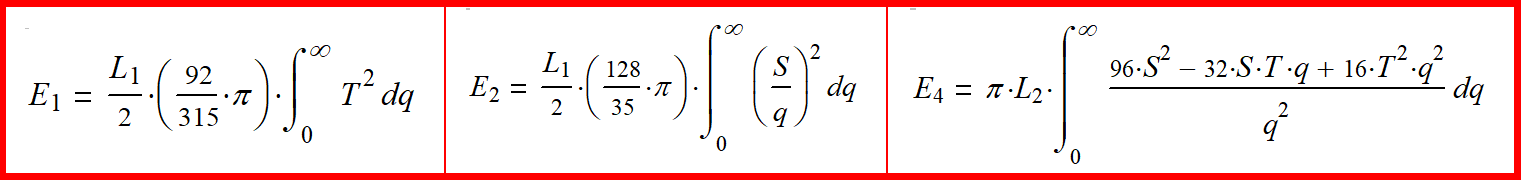Назад    Главная страница     Оглавление     Далее  

Formulas for energy in Loks. j=3.

 http://vixra.org/abs/1804.0097

1. The essence of the hypothesis.
   Our mathematical model is that:
1. The universe is a rigid elastic continuum. This continuum does not have any numeric parameters or constraints. This continuum may not have any mass or density. But by virtue of the law of conservation, it has some resistance to deformations.
2. In this continuum ALWAYS existed and ALWAYS will exist all kinds of waves. The movement of the waves creates the whole picture of the universe that we observe. Including wave vortices create material particles. The mathematical description is attached.
3. All visible and invisible objects of the universe, from large to small, are wave objects in this continuum. All visible and invisible objects of the universe, from large to small, are solutions of the wave equation:

(1-1)

4. All wave objects in the gukuum are described by an algebraic task parameters of elasticity of a solid body and a three-dimensional wave equation. When This simply assumes that these are "small" and "linear" waves. All questions like "what is" does not make sense. Continuum and everything.
5. As physical = letter parameters it is convenient to use the Lame coefficients L₁, L₂, L₃ (these are elementary combinations of the coefficients of compression, shear and torsion of a solid body). There are no numerical restrictions on the Lamé coefficients. Just the coefficients of Lame L₁, L₂, L₃ and everything.
6. Thus, the universe and all the matter contained in it are described only by letters, algebra. However, objects can be compared numerically. For example, the mass of the proton wave vortex can be numerically compared with the mass of the electron wave vortex.
7. All elementary particles, fields, photons, ball lightning, even lightning, dark matter are different types of solutions of the wave equation. So far we know several types of solutions to the wave equation, three spherical and three cylindrical, but perhaps this is not the only way to limit the universe.
8. The nonlinearity that exists in the universe is explained by the law of "winding a linear solution on itself". This is a very important law that makes it possible to understand the formation of elementary particles. As a result of such winding, or layering, the linear solution becomes non-linear and creates all the variety of the material world. This law consists in adding to the integral for the energy a factor  1/r². 

 

2. Calculation of the energy of loks.
   Further everywhere, as in the first part, we work in spherical coordinates.
   So, we take in mind the wave whirlwind = lok, and position it so that the wave rotation occurs around the Z axis. We assume that all the oscillations in the lok occur in the same direction. So it or not we do not know yet. But this assumption is close to the truth. It is true in the first degree of approximation. This is our mathematical model. We locate the locus so that these oscillations in the locus occur along the Z axis, and the wave itself runs around the Z axis. Similarly, the Lok energy moves around the Z axis. And in exactly the same way the movement of the energy of the lok creates an angular momentum = spin.

Fig.1.

Figure 1 shows a fragment of a wave traveling around the Z axis. The oscillations in it are directed along the Z axis. And the wave runs around the Z axis. As will be seen from the following, the carrier frequency (in blue) is constant on the entire wave vire. However, with the distance from the Z axis, the amplitude of the traveling wave changes. In addition, the angular velocity of the wave changes with the distance from the Z axis. That is, the outer layers are lagging behind the inner ones.
    A particular solution of the wave equation, spherical standing waves:

(1-2)

   This formula is obtained from a linear combination of two solutions with different Ф_m(φ).

   i,j,m - whole numbers.  i=1,2,3.  j=0,1,2…  m=0,1,…,j;

   J_j(k•r) - Spherical Bessel functions of the first kind;

   Y_j(θ,φ) - spherical surface harmonics;
   Y_j(θ,φ)=P_jm(cosθ)•Ф_m(φ);
   Ф_m(φ)=sin(m•φ-k•c•t);

   P_jm(cosθ) - The adjoint Legendre function of type 1, of order m and rank  j:

(1-3)

   In the formulas, k is repeatedly found. It is connected only with the actual mass (energy) of the particle, and it is determined by it. This is the link between ω in the vibrational part of the solution and the radial coordinate in the Bessel function:  ω=k•c,  c - speed of light. In Fig. (1-1)  ω=k•c – This is the frequency of the blue sine wave, which "carries" the wave frequency. Also  k=1/λ , where  λ – approximate size of the wave vortex. The physics is such that in each particle (in each solution), due to physical reasons, the frequency of the wave traveling along the circle and its particle size are set. Physical causes are determined by the form of the solution, and the way the solution is wound up on itself, and how the entire system stabilizes to a stable state. Also, particles have excited states. To explore this is the business of the future. This can only be observed. Thus, all further solutions and formulas are an illustration of the actual state in which all the wave vortices are located = loks = elementary particles.

   Since our lok is placed vertically, the following relationships hold. In the solution for the displacement vector  W  there is only one component  W_Z .  W_x  и  W_y  are equal to zero. We have:

(1-4-1)

The following formulas for the transition between Cartesian and spherical coordinates:

(1-4-2)

In this way:

(1-5)

Next, we go for simplicity to the dimensionless length:

(1-6)

We have verified that all loks with j = 2 have a theoretical infinity when calculating energies. Therefore, we missed these loks.
According to mathematical reference books, we have a formula for the bias  W_Z  for the four loks (3,0), (3,1), (3,2) and (3,3):

(1-7)

Useful formulas:

(1-8)

Further, we write out the formulas for the displacements in spherical coordinates:

(1-9)

We have formulas for the strain tensor in spherical coordinates:

(1-10)

The total energy of the lok after all simplifications is expressed by the formula:

(1-11)

Further, we calculate the elements of the strain and energy tensor for each lok separately.

Lok (3,0).
For him, three terms are not zero:

(1-12)

Lok energy (3.0). Here the square of the strain tensor is integrated over the space. The volume element contains a factor  q² , But the law of winding the solution contains  1/q². These factors cancel each other and simplify the integral.

(1-13)

After substituting the value W_i,j by formula (1-12), we obtain three nonzero integrals:

(1-14)

It turns out that all integrals are taken and equal:

(1-15)

Lok (3.0) has an axial symmetry. This can be seen from the formula for the displacement (1-12), there are no angular coordinates φ in it. The graph of radial energy distribution and energy density has the form:

Fig.2.

As can be seen from the graph, Lok (3,0) has a classical seal in the center.

Lok (3.1).
Note that here q is quite different than for lok (3.0).
Non-zero elements of the strain tensor:

(1-16)

The energy of the lok (3.1). The square of the strain tensor is integrated over the space. The volume element contains a factor  q² , But the law of winding the solution contains  1/q². These factors cancel each other and simplify the integral.

(1-17)

After substituting the value W_i,j by formula (1-12), we obtain three nonzero integrals:

(1-18)

It turns out that all integrals are taken and equal:

(1-19)

Lok (3.1) has no axial symmetry. This can be seen from the formula for the displacement (1-16), in it there is an angular coordinate φ. The graph of radial energy distribution and energy density has the form:

Fig.3.

As can be seen from the graph, the lok (3.1) also has a classical compaction in the center.

Lok (3.2).
Note that here q is the same as for loks (3,0) and (3,1).
Non-zero elements of the strain tensor:

(1-20)

The energy of the lok (3.2). Here the square of the strain tensor is integrated over the space. The volume element contains a factor  q² , But the law of winding the solution contains  1/q². These factors cancel each other and simplify the integral.

(1-21)

After substituting the value W_i,j by formula (1-20), we obtain five nonzero integrals:

(1-22)

It turns out that all integrals are taken and equal:

(1-23)

Lok (3.2) does not have axial symmetry. This is seen from the formula for the displacement (1-20), it has the angular coordinate φ. The graph of radial energy distribution and energy density has the form:

Fig.4.

As can be seen from the graph, the lok (3,2) also has a classical compaction in the center.

Lok (3.3).
Note that here q is the same as for loks (3,0), (3,1), (3,2).
Non-zero elements of the strain tensor:

(1-24)

The lok energy is (3.3). Here the square of the strain tensor is integrated over the space. The volume element contains a factor  q² , But the law of winding the solution contains  1/q². These factors cancel each other and simplify the integral.

(1-25)

After substituting the value W_i,j by formula (1-20), we obtain five nonzero integrals:

(1-26)

All the integrals are taken and equal to:

(1-27)

Lok (3,3) does not have axial symmetry. This can be seen from the formula for the displacement (1-24), it has the angular coordinate φ. The graph of radial energy distribution and energy density has the form:

Fig.5.

As can be seen from the graph, Lok (3,3) also has a classical compaction in the center.

   So, Loks (3,0), (3,1), (3,2), (3,3), and also lok (5,0) also have final energy. Large values of integer arguments create serious computer problems. Loki (2,0), (2,1), (2,2) and all Loki (4,0), (4,1), (4,2), (4,3), (4,4) have energy integrals that go to infinity. Of course, this does not mean the physical meaninglessness of these loks. Simply this means that the given solution is not physically stable and creeps into some other solutions described by other solutions (not spherical) of the wave equation.