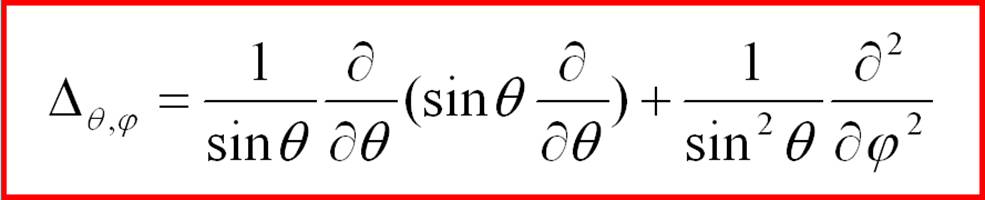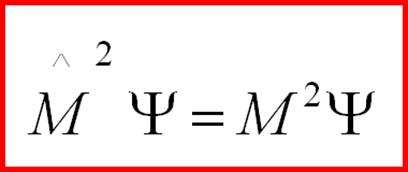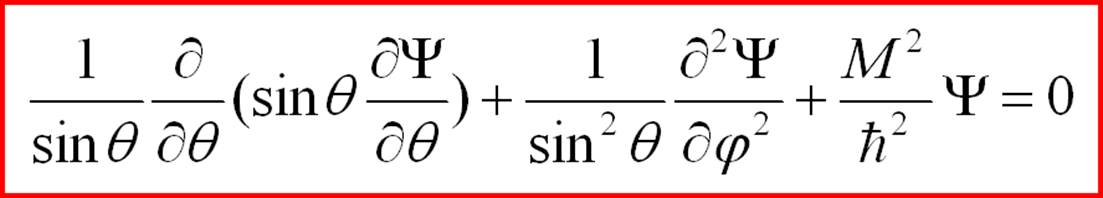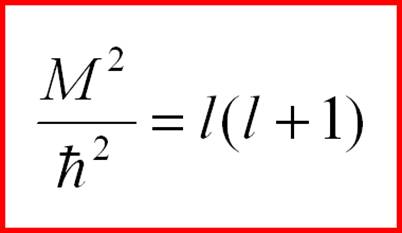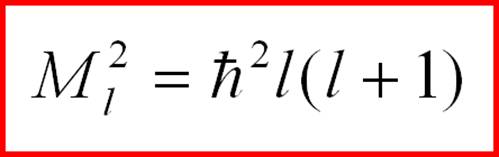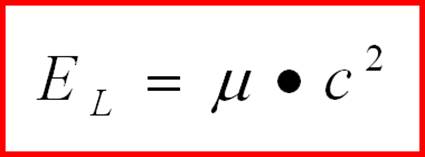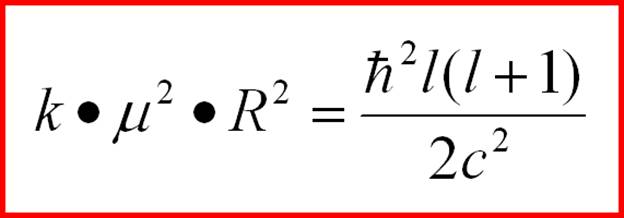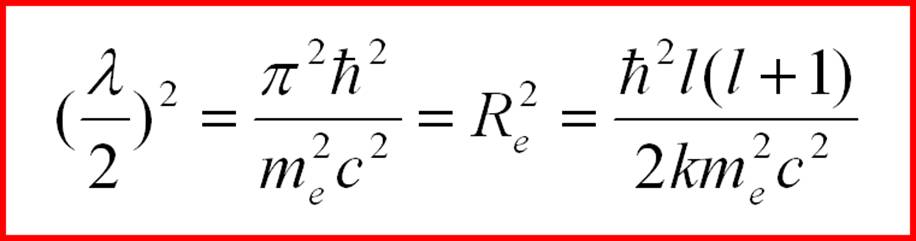|
Назад Главная страница Оглавление Далее The emergence of quantum mechanics in a gukuum. Part 2. Abstract. The energy levels of elementary particles are investigated. The common opinion that free elementary particles do not have energy levels is questioned. Simply, these levels are not yet detected. It is possible that these excited states are not stable. The appearance of a discrete energy spectrum in loks. Let us consider the quantization of the angular momentum of a "microparticle". In the conventional interpretation this quantization is quite abstract, has the character of formal mathematical operations. Nevertheless, this is a generally accepted theory that appears in all textbooks and has the status of an accurate reflection of objective reality. Visualization will only be quantized in gukuum theory. The angular momentum is understood to be the vector product of the radius vector of the particle on its momentum: M=[rp]. In quantum mechanics, the operators of M and p are also multiplied in the same way:
(2-23) We are more interested in the operator of the square of the angular momentum.
(2-24) If we go over to spherical coordinates:
x = r sinθ cosφ, y = r sinθ sinφ, z = r cosθ, (2-25) then for the angular momentum operator we obtain:
(2-26) Where
(2-27) is the Laplace operator for a sphere. Similarly, the projections of the angular momentum operator are obtained depending only on the angular coordinates (θ,φ). The equation for determining the eigenvalues and eigenfunctions of the angular momentum operator of the angular momentum:
(2-28) or substituting (2-26) and (2-27) into (2-28), we obtain the equation:
(2-29) Further in classical quantum mechanics this conclusion follows. The requirement of finiteness, continuity, and uniqueness of the solution (2-29) yields a unique solution. It turns out that such solutions exist only when
(2-30) where l is a positive integer. For each such value of l, there are (2l+1) solutions, which are spherical functions. The eigenvalues of the squared angular momentum operator are:
(2-31) l = 0, 1, 2, … That
is, from the Schrödinger equation (which, as we have shown,
is equivalent to the wave equation) necessarily follows the
discreteness of the square of the angular momentum of the
object, regardless of the appearance of this object. In
particular, these objects can be loks. Moreover, if we
"solve the wave equation" in the forehead, we require
"continuity and uniqueness" of the solution, then, after the
separation of the variables, we inevitably arrive at
equation (2-29). Only there will be a square of torque of
rotation of lok
M2. And it will be
quite rightly said about him that the values of the square
of the angular momentum of the lok will be discrete and
determined by formula (2-31). Physical parameters of elementary particles. Now let's pay attention to the energy of the lok. The above proof of the discreteness of the square of the angular momentum of an object in our gukuum theory is objective and unambiguous. And behind this discreteness, there are other discreteness with necessity. If we take into account the formula of mechanics:
(2-32)
I
is the moment of inertia of the object.
(2-33) l = 1,2,… The energy of the fixed loks can vary. These vortices can absorb energy quanta. And contrary to the existing opinion, it is assumed that free electrons can absorb photons. It is only necessary to do the corresponding experiments, and not to refer to the outdated theoretical calculations. But energy and mass are connected inseparably, therefore, and the mass of loks has a discrete spectrum.Further, if we represent the moment of inertia of the lok in the form
(2-34) where the values on the right side, respectively: k - some coefficient (without special physical meaning, will be refined below), the mass of the lok and the square of its effective size, then taking into account (2-9) in the form
(2-35) and substituting (2-34) and (2-35) in (2-33), we obtain a new formula for the relationship between the particle size, its mass and the degree of its energy excitation:
(2-36) where as before l is equal to any integer. Truth apart from zero, but now we will not focus on this. It can be assumed that in the unexcited state, that is, for l = 1, a formula should be obtained for the Compton wavelength of an elementary particle (2-12). Comparing formulas (2-12) and (2-36), we obtain, for example, for an electron:
(2-37) whence
(2-38)
As you can see, the result does not depend on which lok is
considered, the electron or the proton. As can be seen from
(2-38) and (2-34), the moment of inertia of elementary
particles increases with increasing energy excitation. Опубликовано: https://www.academia.edu/34576327/The_emergence_of_quantum_mechanics_in_a_gukuum._Part_2
Назад Главная страница Оглавление Далее Страница размещена на сайте в мае 2005 года |